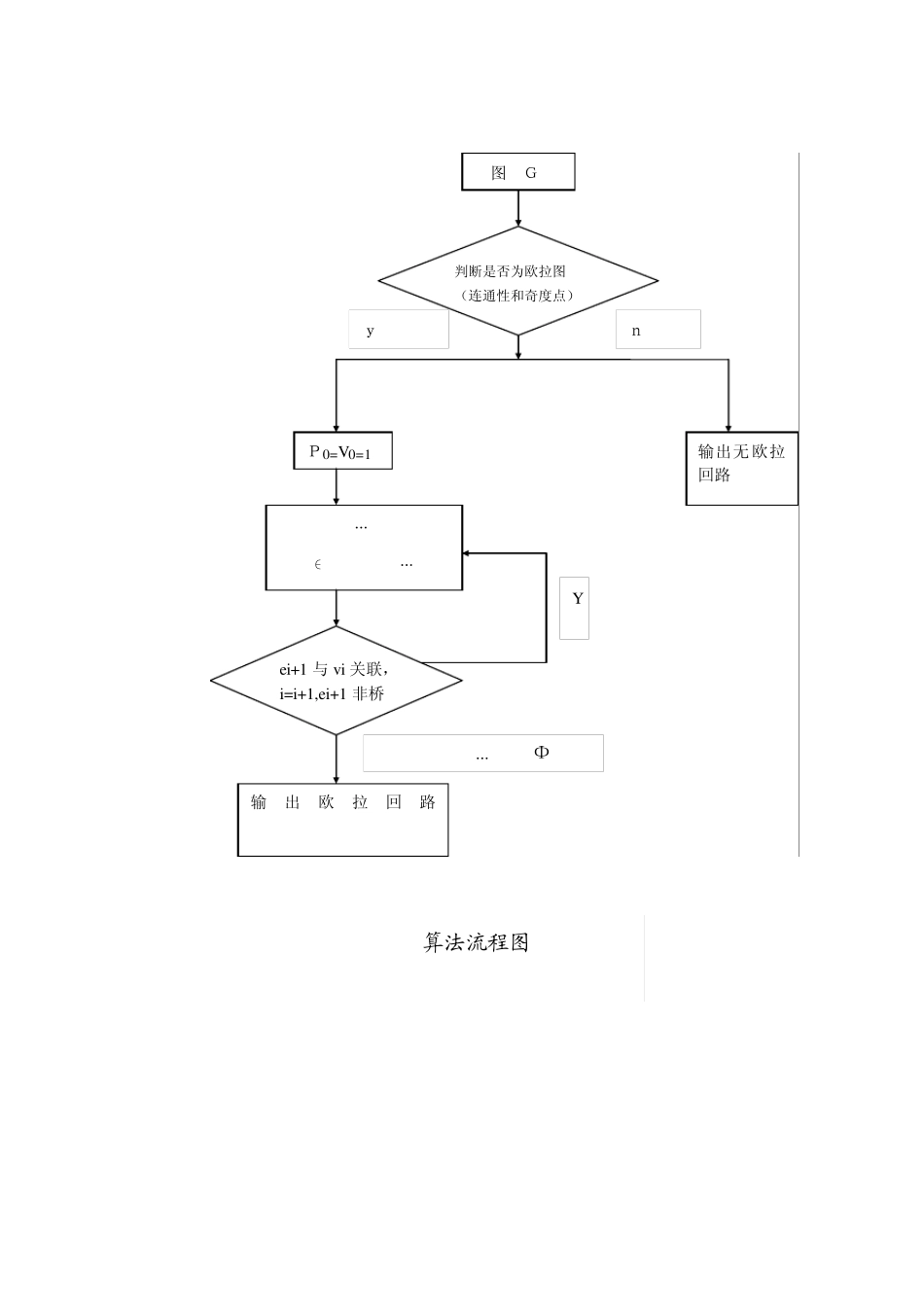
求欧拉回路的Fleury 算法 一、 实验内容: 判断图 G是否存在欧拉回路,若存在,输出其中一条欧拉回路。否则,显示无回路。 二、 实验环境: vc++ 三、 实验过程与结果 1. 问题简介:通过图(无向图或有向图)中所有边一次且仅一次行遍所有顶点的回路称为欧拉回路。具有欧拉回路的图称为欧拉图 2. 算法思想(框图): (1)任取v0∈V(G),令P0=v0. (2)设Pi=v0e1v1e2…eivi已经行遍,按下面方法来从E(G)-{e1,e2,…,ei}中选取ei+1: (a)ei+1与 vi相关联; (b)除 非 无 别 的 边 可 供 行 遍 ,否 则 ei+1不 应 该 为Gi=G-{e1,e2,…,ei}中的桥。 (3)当(2)不能再进行时,算法停止。 可以证明,当算法停止时所得简单回路 Pm=v0e1v1e2…emvm(vm=v0)为 G中一条欧拉回路。 判断是否为欧拉图 (连通性和奇度点) 图 G y n 输出无欧拉回路 P0=V0=1 Pi=v0e1v1…eivi, ei+1∈E(G)-{e1,…,ei} ei+1 与 v i 关联,i=i+1,ei+1 非桥 Y 输出欧拉回路Pm=v0e1v1e2emvm(vm=v0) E(G)-{e1,e2,…,ei}=Φ Fleury算法流程图 3. 数据输入: 边数5,点数6 相关联的点1 2 1 3 2 5 4 2 3 2 4 5 4. 运行结果: 存在欧拉回路 1,3,2,4,5,2,1 5. 分析总结: Fleu ry 算法是求欧拉图的十分有效的算法,在执行过程中需要用到类似于图的深度优先遍历,因为该算法就是需要将已找到的路径不断的扩展下去,直到将所有边扩展进路径。 四、 完整源程序 #include #include #include struct stack { int top , node[81]; } T,F,A; //顶点的堆栈 int M[81][81]; //图的邻接矩阵 int n; int degree[81]; bool brigde(int i,int j) { int flag[81],t,s; for(s=1;s<=n;s++) flag[s]=0; if(degree[i]==1) return false; else { M[i][j]=0;M[j][i]=0; A.top=1; A.node[1]=i; flag[i]=1; t=i; while(A.top>0) { for(s=1;s<=n;s++) { if(degree[s]>0){ if(M[t][s]==1) if(flag[s]==0) { A.top++; A.node[A.top]=s; flag[s]=1; t=s; break; } } } if(s>n){ A.top--; t=A.node[A.top]; } } for(s=1;s<=n;s++) { if(degree[s]>0) if(flag[s]==0) { M[i][j]=M[i][j]=1; return true; break; } } if(s>n) return false; } } void Fleury(int x) //Fleury 算法 { int i...