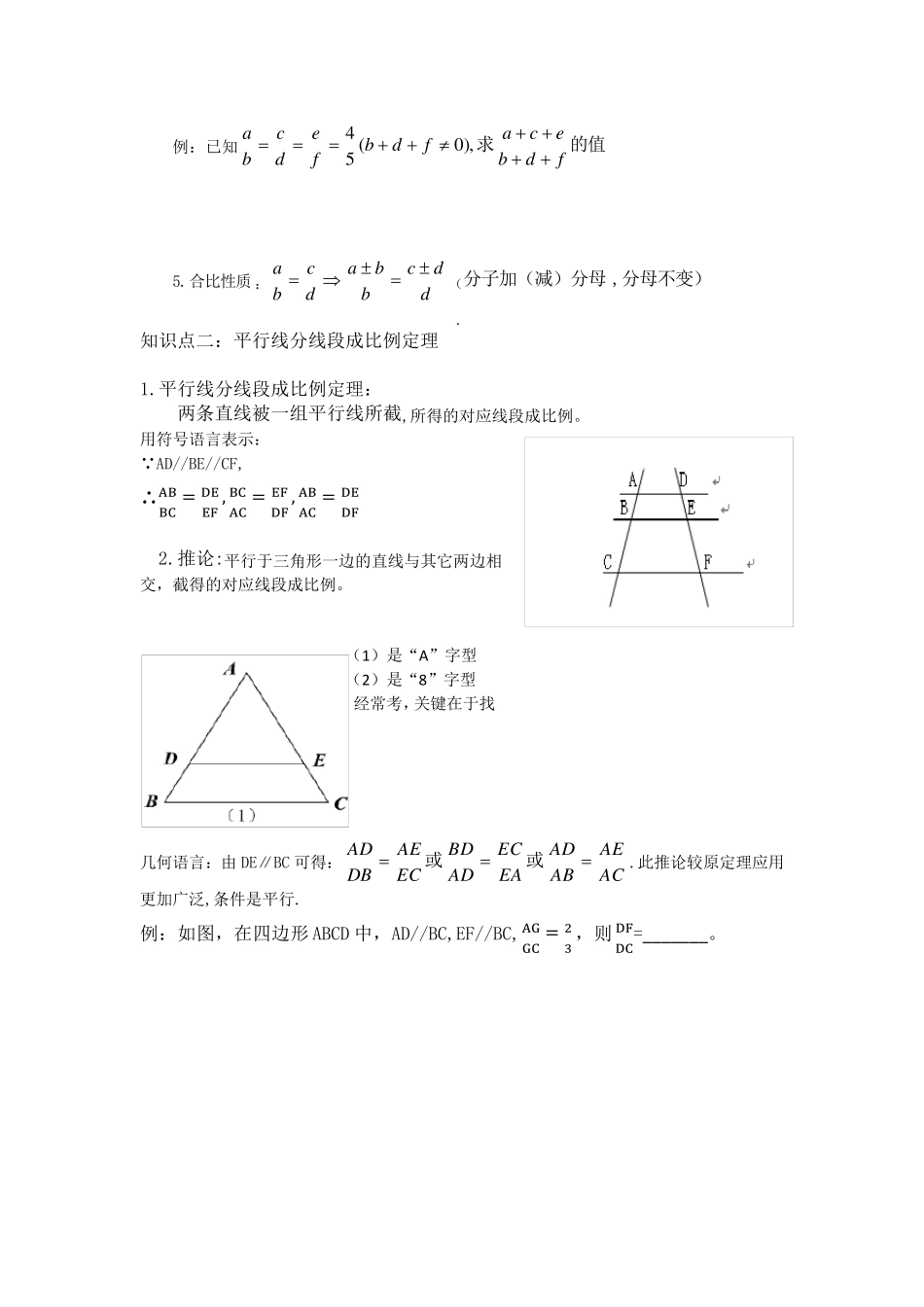
相似三角形培优专题讲义 知识点一:比例线段有关概念及性质 (1)有关概念 1、两条线段的比:选用同一长度单位量得两条线段量得AB、CD 的长度分别是m、n,那么就说这两条线段的比是AB:CD=m:n 例:已知线段AB=2.5m,线段CD=400cm,求线段AB 与CD 的比。 2.比例线段:四条线段a、b、c、d 中,如果a 与b 的比等于c 与d 的比,即dcba (或a:b=c:d),那么,这四条线段a、b、c、d 叫做成比例线段,简称比例线段。(注意:在求线段比时,线段单位要统一,单位不统一应先化成同一单位,还要注意顺序。) 例:b,a,d,c 是成比例线段,其中a=2cm,b=3cm,c=6cm,求线段d 的长度。 (2)比例性质 1.基本性质: bcaddcba (两外项的积等于两内项积) 2.反比性质: cdabdcba (把比的前项、后项交换) 3.更比性质(交换比例的内项或外项): ()()()abcdacdcbdbadbca,交换内项,交换外项.同时交换内外项 4.等比性质:(分子分母分别相加,比值不变.) 如果)0(nfdbnmfedcba,那么banfdbmeca. 注意:(1)此性质的证明运用了“设k 法” ,这种方法是有关比例计算,变形中一种常用方法. (2)应用等比性质时,要考虑到分母是否为零. (3)可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立. 例:已知的值求 fdbecafdbfedcba),0(54 5.合比性质:ddcbbadcba(分子加(减)分母,分母不变) . 知识点二:平行线分线段成比例定理 1.平行线分线段成比例定理: 两条直线被一组平行线所截,所得的对应线段成比例。 用符号语言表示: AD//BE//CF, ∴ABBC = DEEF , BCAC = EFDF , ABAC = DEDF 2.推论:平行于三角形一边的直线与其它两边相交,截得的对应线段成比例。 几何语言:由DE∥BC 可得:ACAEABADEAECADBDECAEDBAD或或.此推论较原定理应用更加广泛,条件是平行. 例:如图,在四边形ABCD 中,AD//BC,EF//BC,AGGC = 23 ,则DFDC=_______。 (1)是“A”字型 (2)是“8”字型 经常考,关键在于找 知识点三:相似形多边形 1.定义:各角分别相等、各边成比列的两个多边形叫做相似多边形。 2.相似多边形的性质:如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边成比例。 3.判定:如果两个多边形的对应边成比列,对应角相等,...