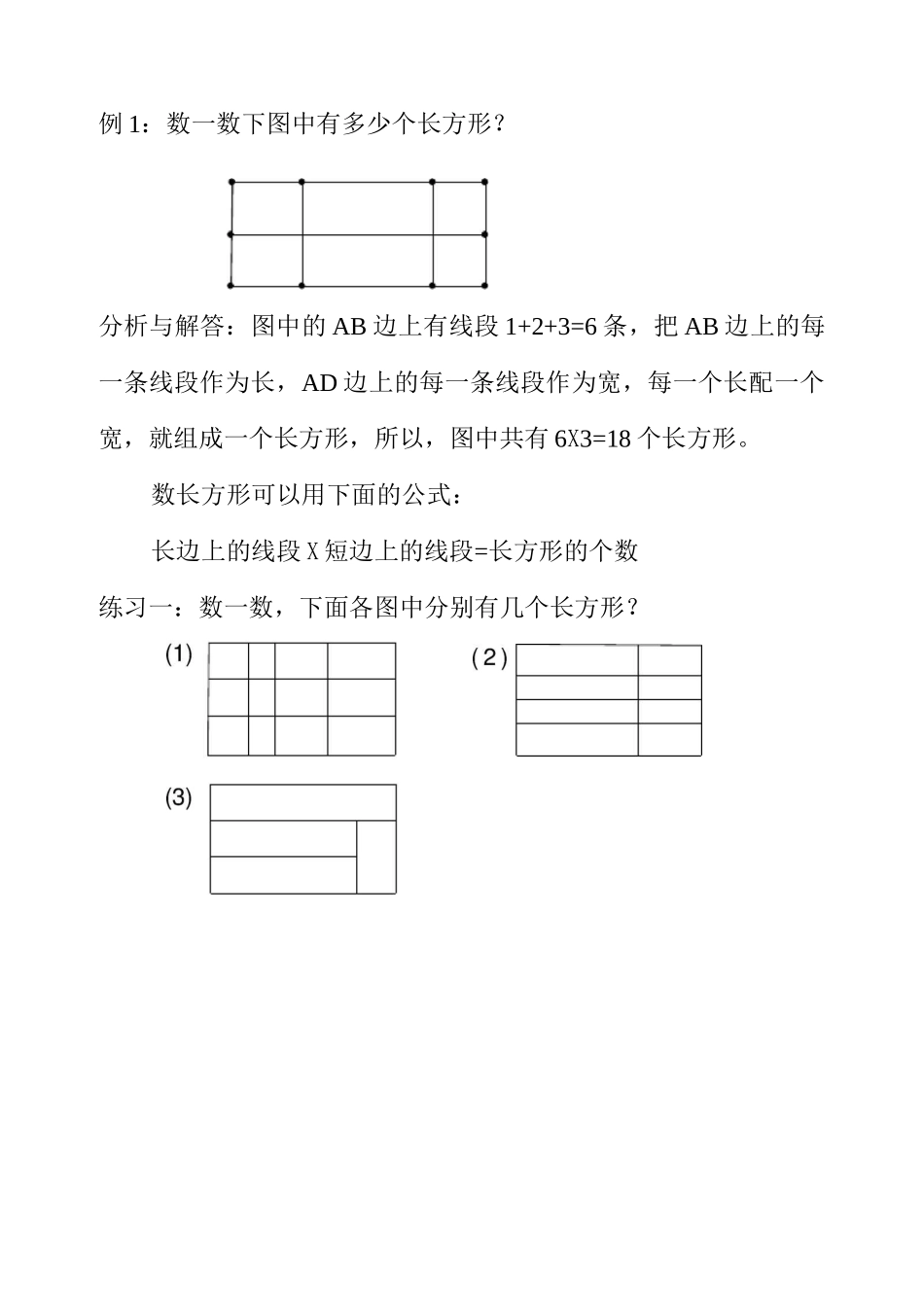
第十八周数数图形(二)专题简析:在解决数图形问题时,首先要认真分析图形的组成规律,根据图形特点选择适当的方法,既可以逐个计数,也可以把图形分成若干个部分,先对每部分按照各自构成的规律数出图形的个数,再把他们的个数合起来。例 1:数一数下图中有多少个长方形?分析与解答:图中的 AB 边上有线段 1+2+3=6 条,把 AB 边上的每一条线段作为长,AD 边上的每一条线段作为宽,每一个长配一个宽,就组成一个长方形,所以,图中共有 6X3=18 个长方形。数长方形可以用下面的公式:长边上的线段 X 短边上的线段=长方形的个数练习一:数一数,下面各图中分别有几个长方形?例 2:数一数,下图中有多少个正方形?(每个小方格是边长为 1的正方形)分析与解答:图中边长为 1 个长度单位的正方形有 3X3=9 个,边长为 2 个长度单位的正方形有 2X2=4 个,边长为 3 个长度单位的正方形有 1X1=1 个。所以图中的正方形总数为:1+4+9=14 个。经进一步分析可以发现,由相同的 nXn 个小方格组成的几行几列的正方形其中所含的正方形总数为:1X1+2X2+・・・+nXn。练习二:数一数下列各图中分别有多少个正方形?(每个小方格为边长是 1 的小正方形)其中有多少个是正方形?2.例 3:数一数下图中有多少个正方形?(其中每个小方格都是边长为 1 个长度单位的正方形)分析与解答:边长是 1 个长度单位的正方形有 3X2=6 个,边长是 2个长度单位的正方形有 2X1=2 个。所以,图中正方形的总数为:6+2=8 个。经进一步分析可以发现,一般情况下,如果一个长方形的长被分成 m 等份,宽被分成 n 等份(长和宽的每一份都是相等的)那么正方形的总数为:mn+(m—1)(n—1)+(m—2)(n—2)(m—n+1)n练习三1.数一数下列各图中分别有多少个正方形。例 4:从广州到北京的某次快车中途要停靠 8 个大站,铁路局要为这次快车准备多少种不同车的车票?这些车票中有多少种不同的票价?分析与解答:这道题是数线段的方法在实际生活中的应用,连同广州、北京在内,这条铁路上共有 10 个站,共有 1+2+3+・・・+9=45条线段,因此要准备 45 种不同的车票。由于这些车站之间的距离各不相等,因此,有多少种不同的车票,就有多少种不同的票价,所以共有 45 种不同的票价。练习四1,从上海到武汉的航运线上,有 9 个停靠码头,航运公司要为这段航运线准备多少种不同的船票?2,从上海至青岛的某次直快列车,中途要停靠 6 个大站,这次...