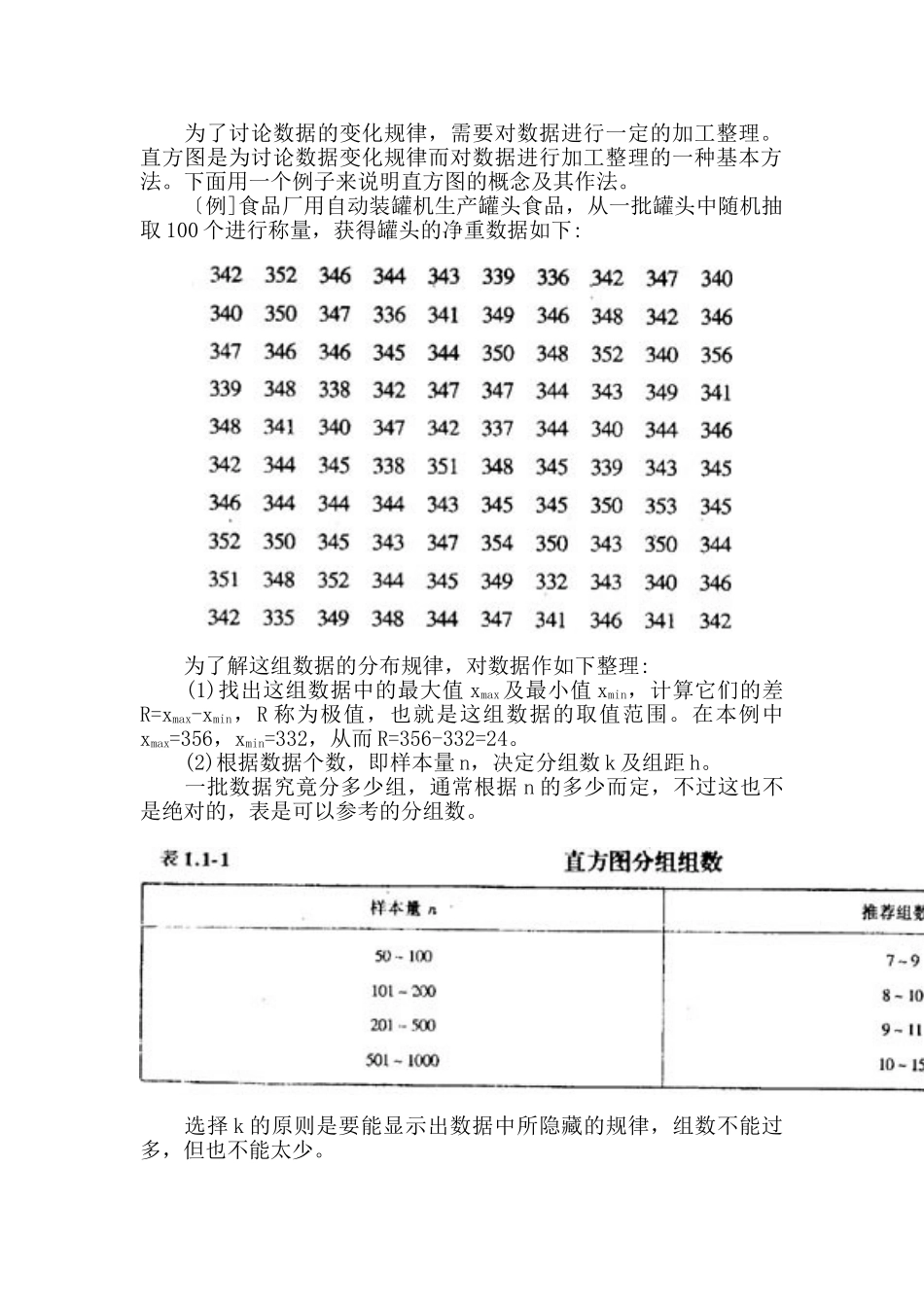
第一章概率统计基础知识??第一节质量特性数据的统计规律? 一、总体、个体与样本 产品的质量可以用一个或多个质量特性来表示。这里的特性可以是定量的,也可以是定性的。例如灯泡的寿命,钢的成分等都是定量特性;而按法律规范判定产品为“合格”或“不合格”,则是一种定性特征。 在质量管理中,通常讨论一个过程中生产的全体产品。在统计中,将讨论、考察对象的全体称为总体。例如某个工厂在一个月内根据一定材料及一定工艺生产的一批灯泡。总体是由个体组成的。在上例中,这批灯泡中的每个特定的灯泡都是一个个体。假如总体中包含的个体数不大,而对产品质量特性的观测(例如测量)手段不是破坏性的,工作量也不大,那么有可能对总体中的每个个体都进行观测,以得到每个个体的质量特性值。但是假如总体中的个体数N 很大,甚至是无限的,或者观测是破坏性的或观测的费用很大,那么不可能对总体中的每个个体都进行观测。通常的做法是从总体中抽取一个或多个个体来进行观测。抽出来的这一部分个体组成一个样本,样本中所包含的个体数目称为样本量。通过对样本的观测来对总体特性进行讨论,是统计的核心。 上述总体、个体和样本的概念是统计的基本概念,从上面的叙述中,这些概念都可以是具体的产品。但有时为了表达的方便,当讨论产品某个特定的质量特性 X 时,也常把全体产品的特性看做为总体,而把一个具体产品的特性值 x 视为个体,把从总体中抽出的由 n 个产品的特性值 x1,x2,…,xn看做为一个样本。 [例]从一个工厂一个月内生产的一批灯泡中抽取 n=8 个灯泡,进行寿命试验,得到这 8 个灯泡的使用寿命为(单位为小时): 325,84,1244,870,645,1423,1071,992 这 8 个灯泡或相应的使用寿命即为一个样本,样本量 n=8。 从总体中抽取样本的方法称为抽样。为使抽取的样本对总体有代表性,样本不能是有选择的,最好应是随机抽取的,关于这一点,以后我们还要详细解释。 二、频数(频率)直方图及累积频数(频率)直方图 为讨论一批产品的质量情况,需要讨论它的某个质量特性(这里为了叙述简单起见,仅讨论一个质量特性,有必要时也可以同时讨论多个质量特性)X 的变化规律。为此,从这批产品(总体)中抽取一个样本(设样本量为 n),对每个样本产品进行该特性的测量(观测)后得到一组样本观测值,记为 x1,x2,…,xn,这便是我们通常说的数据。 为了讨论数据的变化规律,需要对数据进行一定的加工整理。直方图是为讨论数据...