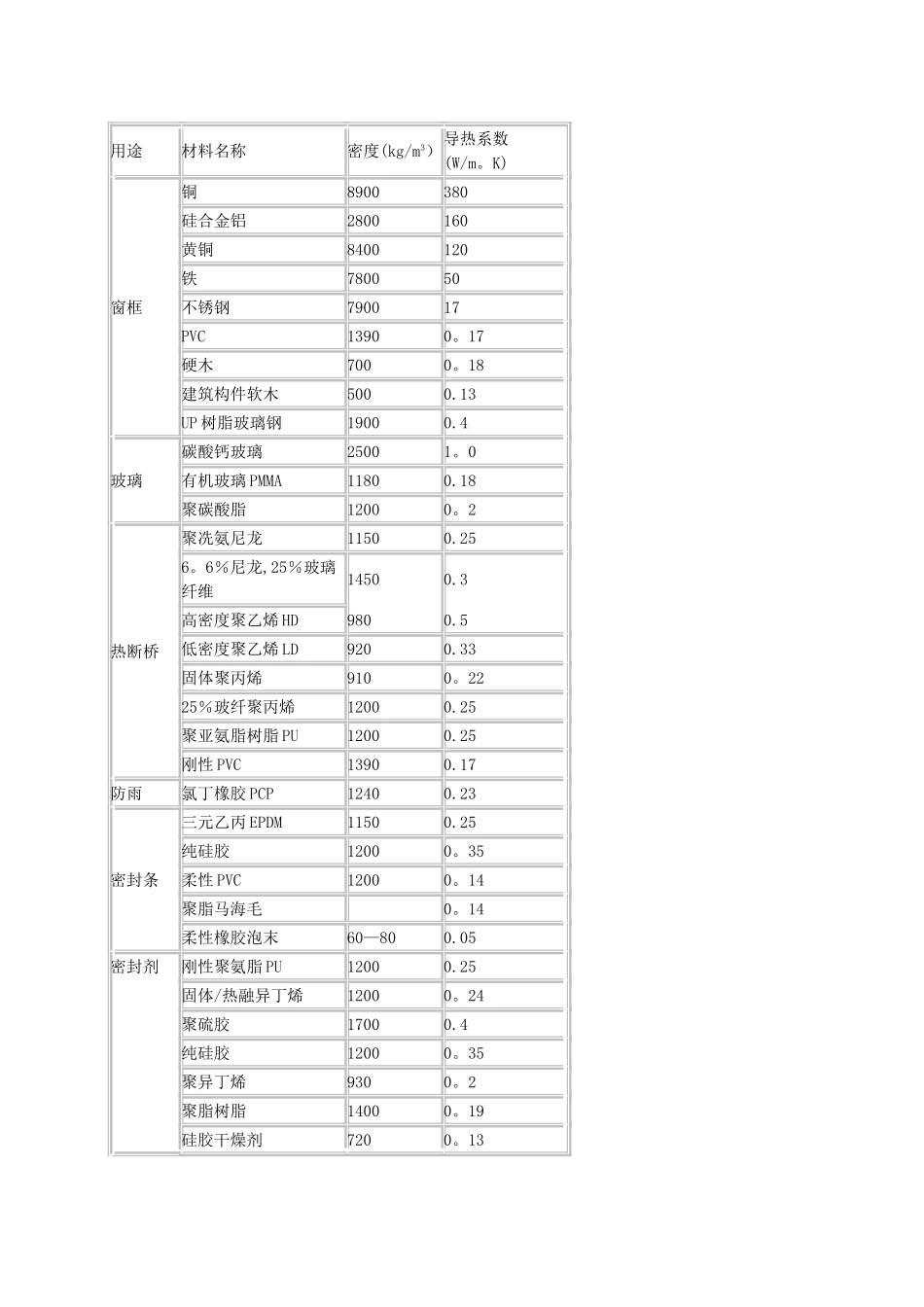
材料的导热率傅力叶方程式:Q=KA△T/d,R=A△T/Q Q: 热量,W;K: 导热率,W/mk;A:接触面积;d: 热量传递距离;△T:温度差;R: 热阻值导热率 K 是材料本身的固有性能参数,用于描述材料的导热能力.这个特性跟材料本身的大小、形状、厚度都是没有关系的,只是跟材料本身的成分有关系.所以同类材料的导热率都是一样的,并不会因为厚度不一样而变化.将上面两个公式合并,可以得到 K=d/R。因为 K 值是不变的,可以看得出热阻 R 值,同材料厚度 d 是成正比的。也就说材料越厚,热阻越大.但假如认真看一些导热材料的资料,会发现很多导热材料的热阻值 R,同厚度 d 并不是完全成正比关系。这是因为导热材料大都不是单一成分组成,相应会有非线性变化。厚度增加,热阻值一定会增大,但不一定是完全成正比的线性关系,可能是更陡的曲线关系。根据 R=A△T/Q 这个公式,理论上来讲就能测试并计算出一个材料的热阻值 R.但是这个公式只是一个最基本的理想化的公式,他设定的条件是:接触面是完全光滑和平整的,所有热量全部通过热传导的方式经过材料,并达到另一端。实际这是不可能的条件.所以测试并计算出来的热阻值并不完全是材料本身的热阻值,应该是材料本身的热阻值+所谓接触面热阻值。因为接触面的平整度、光滑或者粗糙、以及安装紧固的压力大小不同,就会产生不同的接触面热阻值,也会得出不同的总热阻值。所以国际上流行会认可设定一种标准的测试方法和条件,就是在资料上常常会看到的 ASTM D5470.这个测试方法会说明进行热阻测试时候,选用多大的接触面积 A,多大的热量值 Q,以及施加到接触面的压力数值。大家都使用同样的方法来测试不同 的材料,而得出的结果,才有相比较的意义。通过测试得出的热阻 R 值,并不完全是真实的热阻值.物理科学就是这样,很多参数是无法真正的量化的,只是一个“模糊"的数学概念。通过这样的“模糊"数据,人们可以将一些数据量化,而用于实际应用。 此处所说的“模糊" 是数学术语,“模糊"表示最为接近真实的近似.而同样道理,根据热阻值以及厚度,再计算出来的导热率 K 值,也并不完全是真正的导热率值。傅力叶方程式,是一个完全理想化的公式.我们可用来理解导热材料的原理。但实际应用、热阻计算是复杂的数学模型,会有很多的修正公式,来完善所有的环节可能出现的问题.总之:a 。 同样的材料 , 导热率是一个不变的数值,热阻值是会随厚度发生变化的。 b. 同样的材料,厚度越大,可简单理解...