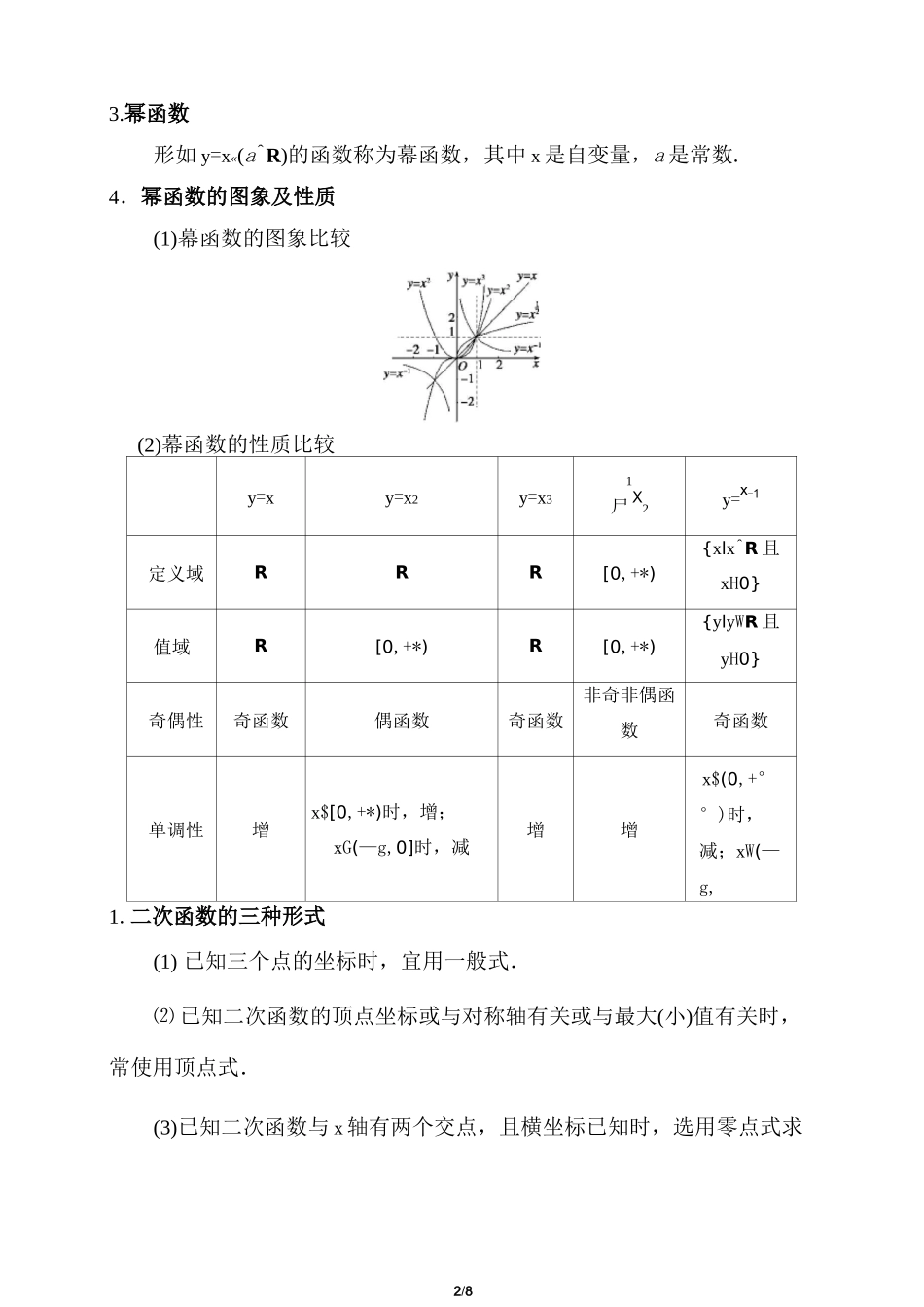
1/8二次函数与幂函数的知识点总结与题型归纳1.二次函数的定义与解析式(1)二次函数的定义形如:f(x)=ax2+bx+c_(a#0)的函数叫作二次函数.(2)二次函数解析式的三种形式① 一般式:fx)=ax2+bx+c_(aH0).② 顶点式::f(x)=a(x—m)2+n(a#0).③ 零点式:f(x)=a(x—xx)(x—x2)_(a#0).2.二次函数的图象和性质解析式f(x)=ax2+bx+c(a>0)f(x)=ax2+bx+c(a<0)图象定义域(—x,+x)(一 o,+o)「4ac—b2)(4ac—b2~|值域L4a,十丿k4a」在 xefo,上单调递(bnk2a」在 xelo,上单调递减;\厶 Li」单调性「b、增;在 xe,+ol 上单调递「b\L2a 丿在 xe,+ol 上单调递减增L 厶 w 丿奇偶性当 b=0 时为偶函数, bH0 时为非奇非偶函数(b4ac—b2)顶点k2a,4a 丿对称性b图象关于直线 x=—佥成轴对称图形2/83.幂函数形如 y=x«(a^R)的函数称为幕函数,其中 x 是自变量,a 是常数.4.幂函数的图象及性质(1)幕函数的图象比较(2)幕函数的性质比较y=xy=x2y=x31尸 X2y=x-1定义域RRR[0,+*){xlx^R 且xH0}值域R[0,+*)R[0,+*){ylyWR 且yH0}奇偶性奇函数偶函数奇函数非奇非偶函数奇函数单调性增x$[0,+*)时,增;xG(—g,0]时,减增增x$(0,+°°)时,减;xW(—g,0)时,减1.二次函数的三种形式(1) 已知三个点的坐标时,宜用一般式.⑵ 已知二次函数的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式.(3)已知二次函数与 x 轴有两个交点,且横坐标已知时,选用零点式求依题意3/84a+2b+c 二-1,a-b+c 二-1,解之,得]a=-4,4ac-b2f(x)更方便.2.幂函数的图象(1)在(0,1)上,幕函数中指数越大,函数图象越靠近 X 轴,在(1,+-)上幕函数中指数越大,函数图象越远离 X 轴.(2)函数 y=x,y=x2,y=X3,y=xl,y=x-i可作为硏究和学习幕函数图象和性质的代表.题型一求二次函数的解析式【例 1】已知二次函数 f(x)满足 f(2)=-1,f(~1)=~1,且 f(x)的最大值是 8,试确定此二次函数.思维启迪:确定二次函数采用待定系数法,有三种形式,可根据条件灵活运用.解方法一设 f(x)=ax2+bx+c(QHO),vc=7,・••所求二次函数解析式为 f(x)二-4x2+4x+7.方法二设 f(x)二 a(x-m)2+n,aH0.,<f(2)-1),又根据题意函数有最大值为 n=8,••y=fx)=a(X-2)2+8«•.•f(2)=-1,Aa(x-1)2+8=-1,解之,得 a=-4.24/8:.f(x)=-4(x-i)2+8 二-4x2+4x+7.2方法三依题意知,f(x)+1=0 的两根为x=2,x=-1,古攵可设 f(x)+1=a(x-2)(x+1),a#0.12即 f(x)二 ax2-ax-2a-1.又函数有最大值 y 二 8,...