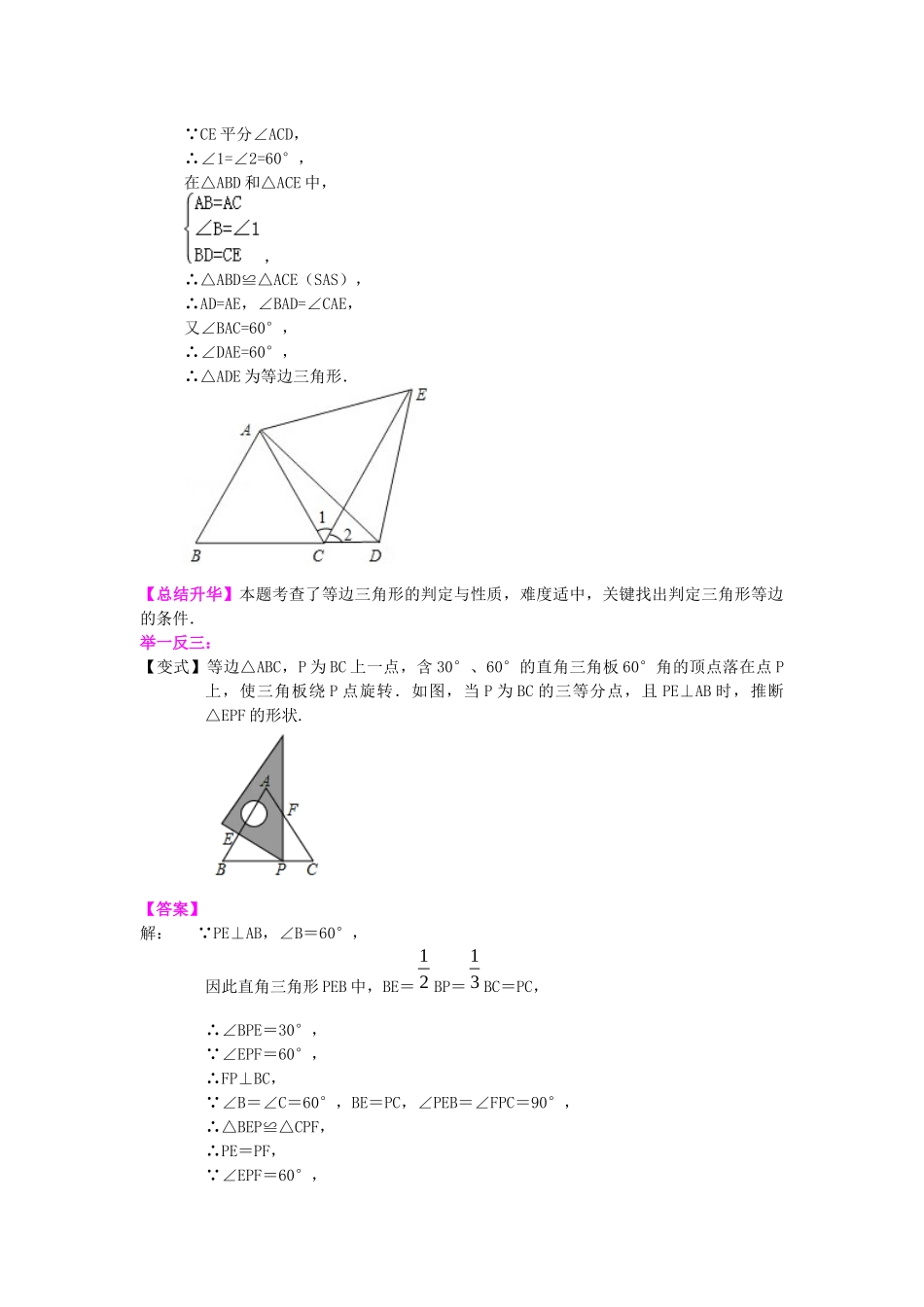
等边三角形(基础)【学习目标】1. 掌握等边三角形的性质和判定.2. 掌握含 30°角的直角三角形的一个主要性质.3. 熟练运用等边三角形的判定定理与性质定理进行推理和计算.【要点梳理】要点一、等边三角形等边三角形定义:三边都相等的三角形叫等边三角形. 要点诠释:由定义可知,等边三角形是一种特别的等腰三角形.也就是说等腰三角形包括等边三角形.要点二、等边三角形的性质等边三角形的性质:等边三角形三个内角都相等,并且每一个内角都等于 60°.要点三、等边三角形的判定等边三角形的判定: (1)三条边都相等的三角形是等边三角形;(2)三个角都相等的三角形是等边三角形;(3)有一个角是 60°的等腰三角形是等边三角形.要点四、含 30°的直角三角形含 30°的直角三角形的性质定理:在直角三角形中,假如有一个锐角是 30°,那么它所对的直角边等于斜边的一半. 要点诠释:这个定理的前提条件是“在直角三角形中”,是证明直角三角形中一边等于另一边(斜边)的一半的重要方法之一,通常用于证明边的倍数关系.【典型例题】类型一、等边三角形1、(2024 秋•崇州市期末)如图,已知△ABC 为等边三角形,D 为 BC 延长线上的一点,CE 平分∠ACD,CE=BD,求证:△ADE 为等边三角形.【思路点拨】由条件可以容易证明△ABD≌△ACE,进一步得出 AD=AE,∠BAD=∠CAE,加上∠DAE=60°,即可证明△ADE 为等边三角形.【答案与解析】证明: △ABC 为等边三角形,∴∠B=∠ACB=60°,AB=AC,即∠ACD=120°, CE 平分∠ACD,∴∠1=∠2=60°,在△ABD 和△ACE 中,,∴△ABD≌△ACE(SAS),∴AD=AE,∠BAD=∠CAE,又∠BAC=60°,∴∠DAE=60°,∴△ADE 为等边三角形.【总结升华】本题考查了等边三角形的判定与性质,难度适中,关键找出判定三角形等边的条件.举一反三:【变式】等边△ABC,P 为 BC 上一点,含 30°、60°的直角三角板 60°角的顶点落在点 P上,使三角板绕 P 点旋转.如图,当 P 为 BC 的三等分点,且 PE⊥AB 时,推断△EPF 的形状.【答案】解: PE⊥AB,∠B=60°,因此直角三角形 PEB 中,BE=BP=BC=PC,∴∠BPE=30°, ∠EPF=60°,∴FP⊥BC, ∠B=∠C=60°,BE=PC,∠PEB=∠FPC=90°,∴△BEP≌△CPF,∴PE=PF, ∠EPF=60°,1213∴△EPF 是等边三角形.2、已知:如图,△ABC 中,AB=AC,∠ABC=60°,AD=CE,求∠BPD 的度数.【答案与解析】证明:在中,AB...