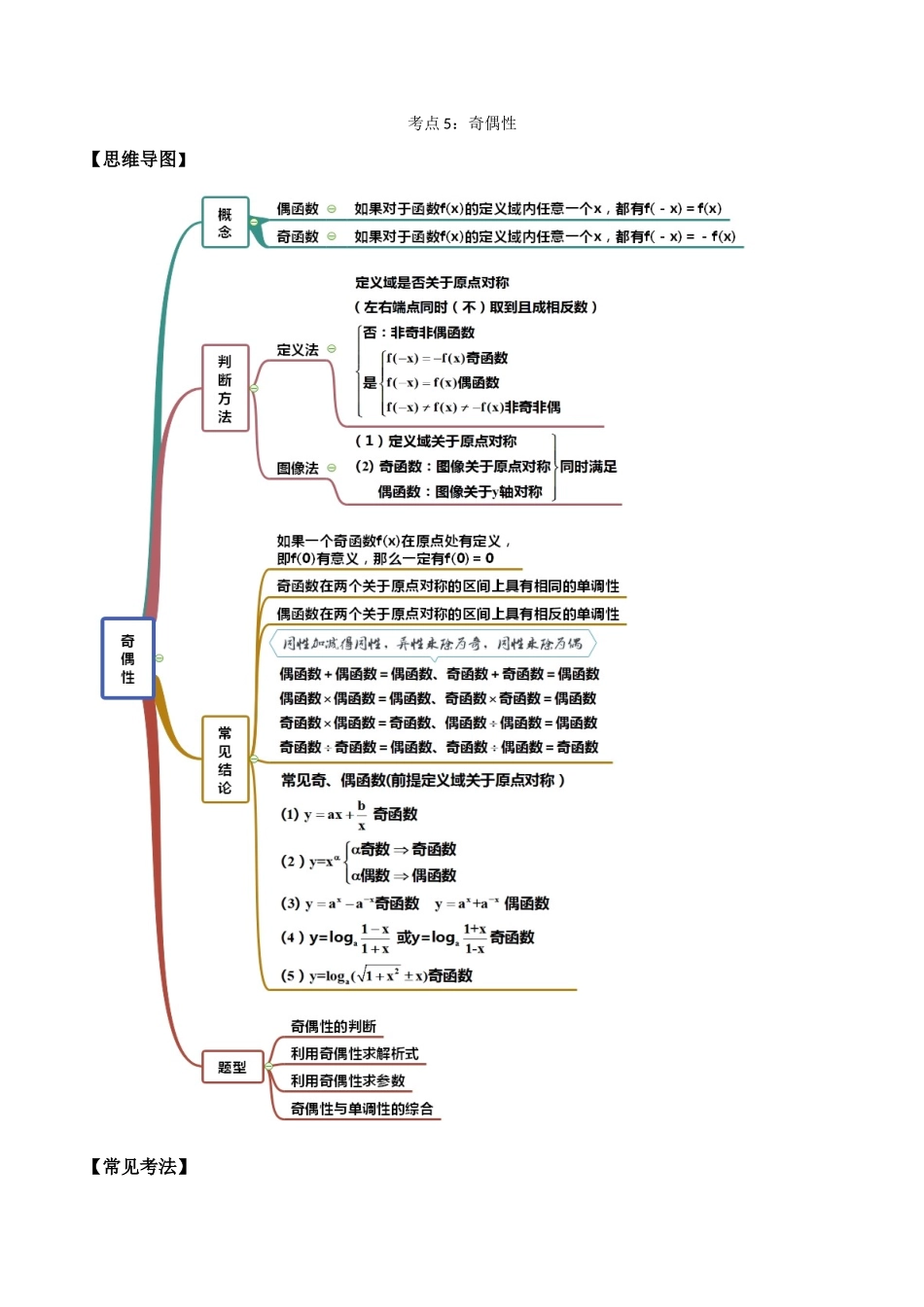
考点 5:奇偶性【思维导图】【常见考法】考法一:奇偶性的推断1.下列函数中,既是奇函数,又在区间上递增的是( )A. B. C. D.【答案】C【解析】对 A, 为偶函数.故 A 错误.对 B, 为非奇非偶函数函数,故 B 错误.对 C, 为奇函数且在上递增.故 C 正确.对 D, 为奇函数但在先减再增,故 D 错误.故选:C2.下列函数是偶函数,且在上是增函数的是( )A. B. C. D.【答案】C【解析】对于:,,所以不是偶函数;对于:,,是偶函数,但是根据幂函数的性质可知,在上是减函数;对于:,是偶函数,当时在上是增函数,符合题意;对于:,所以不是偶函数,故选:C.考点二:利用奇偶性求解析式1.已知 f(x)是定义在 R 上的奇函数,当 x>0 时,f(x)=x2-4x,则 f(x)= ________ .【答案】【解析】 f(x)是定义在 R 上的奇函数,∴f(0)=0.又当 x<0 时,-x>0,∴f(-x)=x2+4x.又 f(x)为奇函数,∴f(-x)=-f(x),则 f(x)=-x2-4x(x<0),∴f(x)=2.已知是偶函数,若当时,,则当时, .【答案】【解析】当时,,是偶函数当时,则, 所以当时,考点三:求参数1.若函数为奇函数,则= .【答案】【解析】由函数 f(x)为奇函可得,f(﹣x)=f﹣ (x)∴=,∴5x﹣(4x3﹣ )(x+a)=5x﹣(4x+3)(xa﹣ )∴(4a3﹣ )x2=0∴4a3=0﹣即 a=2.若函数是定义在上的偶函数,则的值域为 . 【答案】【解析】依题意为偶函数,所以,解得,所以.另,即,,所以,根据二次函数的性质可知,当时,函数有最大值为,当时,函数有最小值为 .所以函数的值域为.3.若函数是奇函数,则 。【答案】【解析】由得,∴,∴.4.已知函数为偶函数,则 。【答案】【解析】由题意,函数为偶函数,又由函数为奇函数,所以函数为奇函数,则,得,所以,得,所以。考点四:奇偶性与单调性的综合1.已知函数为偶函数,当时,,则( )A.B.C.D.【答案】D【解析】,令,.当时,,单调递增;当时,,单调递减.因为,所以当时,,且单调递增.又,所以,在上单调递减,且故.故选:2.已知函数,,若,则 a,b,c 的大小关系为( )A.a