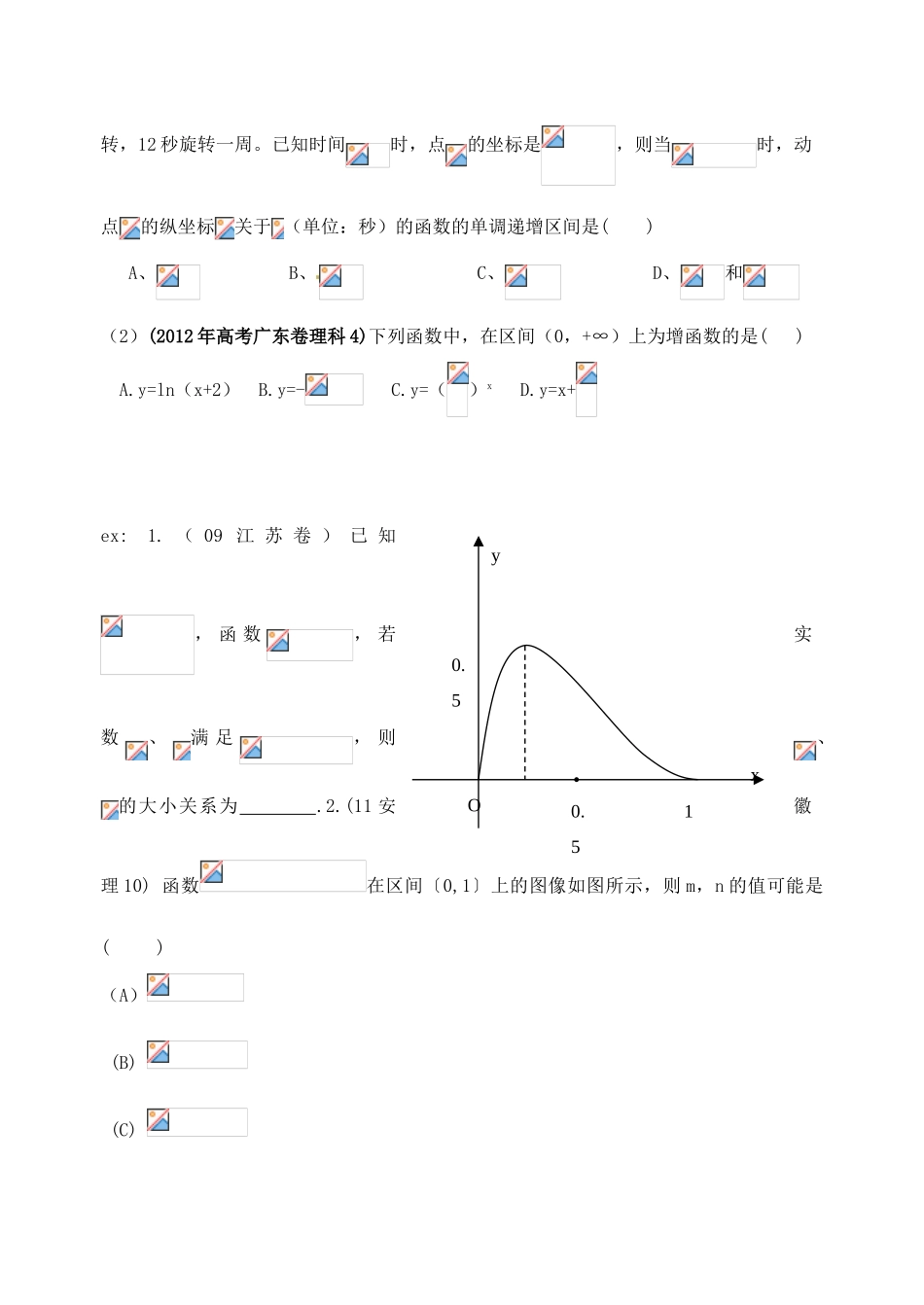
广东省佛山市中大附中三水实验中学高三数学《2.3 函数的单调性与最值 》基础复习学案 新人教 A 版 [研读考纲][知识梳理][备考建议]本讲复习首先回扣课本,从“数”与“形”两个角度来把握函数的单调性和最值的概念,复习中重点掌握:(1)函数单调性的判断及其应用;(2)求函数最值的各种基本方法;对常见题型的解法要熟练掌握.[方法提示]一个防范函数的单调性是对某个区间而言的,所以要受到区间的限制.例如函数 y=分别在(-∞,0),(0,+∞)内都是单调递减的,但不能说它在整个定义域即(-∞,0)∪(0,+∞)内单调递减,只能分开写,即函数的单调减区间为(-∞, 0)和(0,+∞),不能用“∪”连接.两种形式设任意 x1,x2∈[a,b]且 x1<x2,那么①>0⇔f(x)在[a,b]上是增函数;<0⇔f(x)在[a,b]上是减函数.②(x1 -x2)[f(x1)-f(x2)]>0⇔f(x)在[a,b]上是增函数;(x1-x2)[f(x1)-f(x2)]<0⇔f(x)在[a,b]上是减函数.两条结论(1)闭区间上的连续函数一定存在最大值和最小值.当函数在闭区间上单调时最值一定在端点取到.(2)开区间上的“单峰”函数一定存在最大(小)值.四种方法函数单调性的判断:(1)定义法:取值、作差、变形、定号、下结论.(2)复合法:同增异减,即内外函数的单调性相同时,为增函数,不同时为减函数.(3)导数法:利用导数研究函数的单调性.(4)图象法:利用图象研究函数的单调性.[考向训练]一、函数单调性例(1)(10 安徽理 9)动点在圆上绕坐标原点沿逆时针方向匀速旋转,12 秒旋转一周。已知时间时,点的坐标是,则当时,动点的纵坐标关于 (单位:秒)的函数的单调递增区间是( ) A、B、C、D、和(2)(2012 年高考广东卷理科 4)下列函数中,在区间(0,+∞)上为增函数的是( ) A.y=ln(x+2) B.y=- C.y=()x D.y=x+ ex: 1. ( 09 江 苏 卷 ) 已 知, 函 数, 若实数、满 足, 则、的大小关系为 .2.(11 安徽理 10) 函数在区间〔0,1〕上的图像如图所示,则 m,n 的值可能是 ( )(A) (B) (C) y0.51xO0.5 (D) 3.已知函数f(x)=(a 是常数且 a>0).对于下列命题:(1)函数 f(x)的最小值是-1.(2)函数 f(x)在 R 上是单调函数.(3)若 f(x)>0 在[1/2,+)上恒成立,则 a 的取值范围是 a>1.(4)对任意其中正确命题的序号是 4.(11 上海理 16)下列函数中,既是偶函数,又是在区间上单调递减的函数是( )(A). (B). (C). (D).5.设 f(x)为...