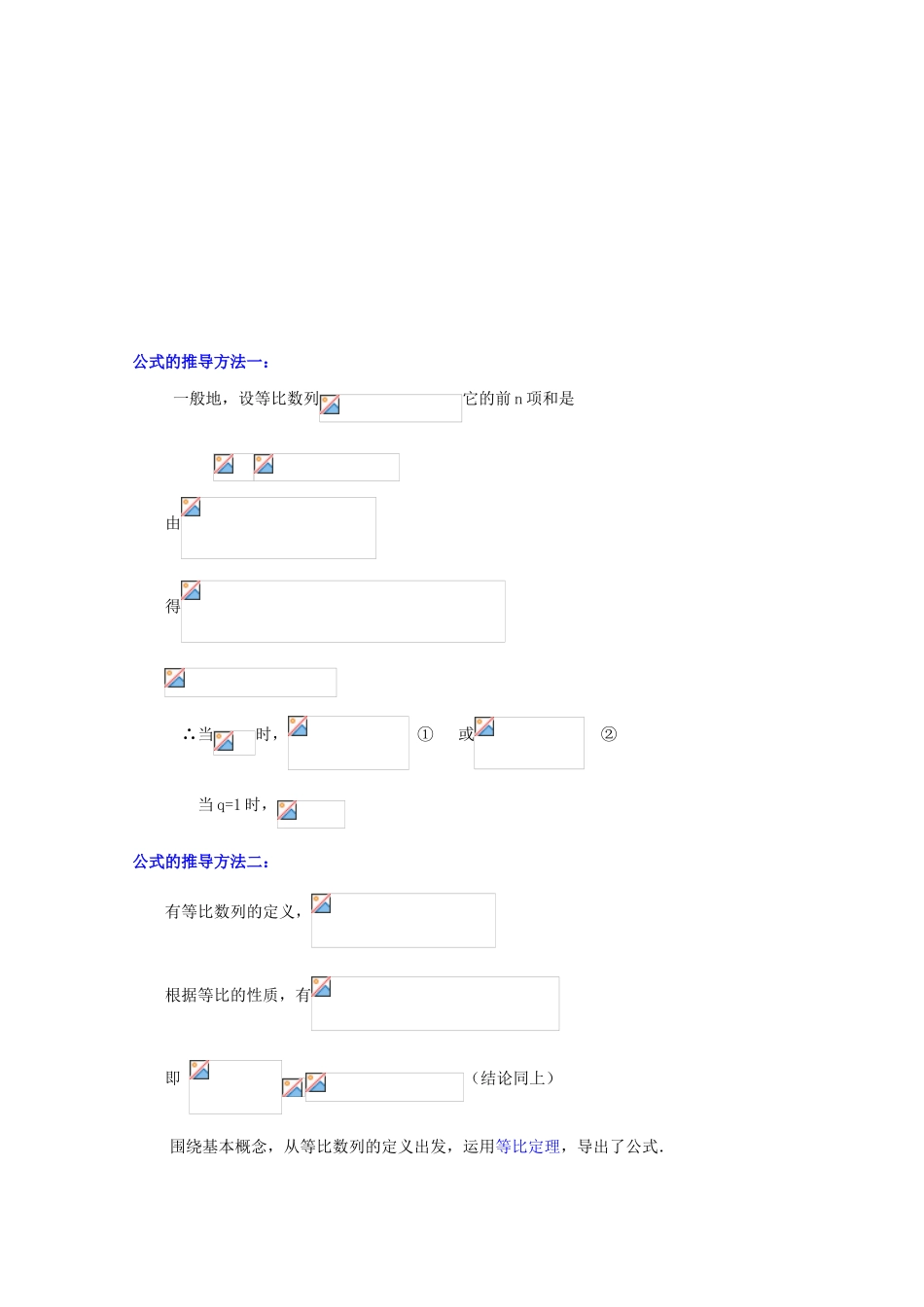
贵州省贵大附中 2011 届数学复习教学案:3.5 等比数列的前 n 项和(1)教学目的:1.掌握等比数列的前 n 项和公式及公式证明思路.2.会用等比数列的前 n 项和公式解决有关等比数列的一些简单问题教学重点:等比数列的前 n 项和公式推导教学难点:灵活应用公式解决有关问题授课类型:新授课课时安排:1 课时教 具:多媒体、实物投影仪教材分析:本节是对公式的教学,要充分揭示公式之间的内在联系,掌握与理解公式的来龙去脉,掌握公式的导出方法,理解公式的成立条件.也就是让学生对本课要学习的新知识有一个清晰的、完整的认识、忽视公式的推导和条件,直接记忆公式的结论是降低教学要求,违背教学规律的做法教学过程:一、复习引入:首先回忆一下前两节课所学主要内容:1.等比数列:如果一个数列从第二项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列 .这个常数叫做等比数列的公比;公比通常用字母 q 表示(q≠0),即:=q(q≠0)2.等比数列的通项公式: , 3.{}成等比数列=q(,q≠0) “≠0”是数列{}成等比数列的必要非充分条件4.既是等差又是等比数列的数列:非零常数列. 5.等比中项:G 为 a 与 b 的等比中项. 即 G=±(a,b 同号).6.性质:若 m+n=p+q,7.判断等比数列的方法:定义法,中项法,通项公式法8.等比数列的增减性:当 q>1, >0 或 01, <0,或 00 时, {}是递减数列;当 q=1 时, {}是常数列;当 q<0 时, {}是摆动数列; 二、讲解新课: 例如求数列 1,2,4,…262,263的各项和即求以 1 为首项,2 为公比的等比数列的前 64 项的和,可表示为: ①2 ②由②—①可得:这种求和方法称为“错位相减法” “错位相减法”,是研究数列求和的一个重要方法等比数列的前 n 项和公式: ∴当时, ① 或 ②当 q=1 时,当已知, q, n 时用公式①;当已知, q, 时,用公式②.公式的推导方法一:一般地,设等比数列它的前 n 项和是由得 ∴当时, ① 或 ②当 q=1 时,公式的推导方法二:有等比数列的定义,根据等比的性质,有即 (结论同上)围绕基本概念,从等比数列的定义出发,运用等比定理,导出了公式.公式的推导方法三: = ==(结论同上) “方程”在代数课程里占有重要的地位,方程思想是应用十分广泛的一种数学思想,利用方程思想,在已知量和未知量之间搭起桥梁,使问题得...