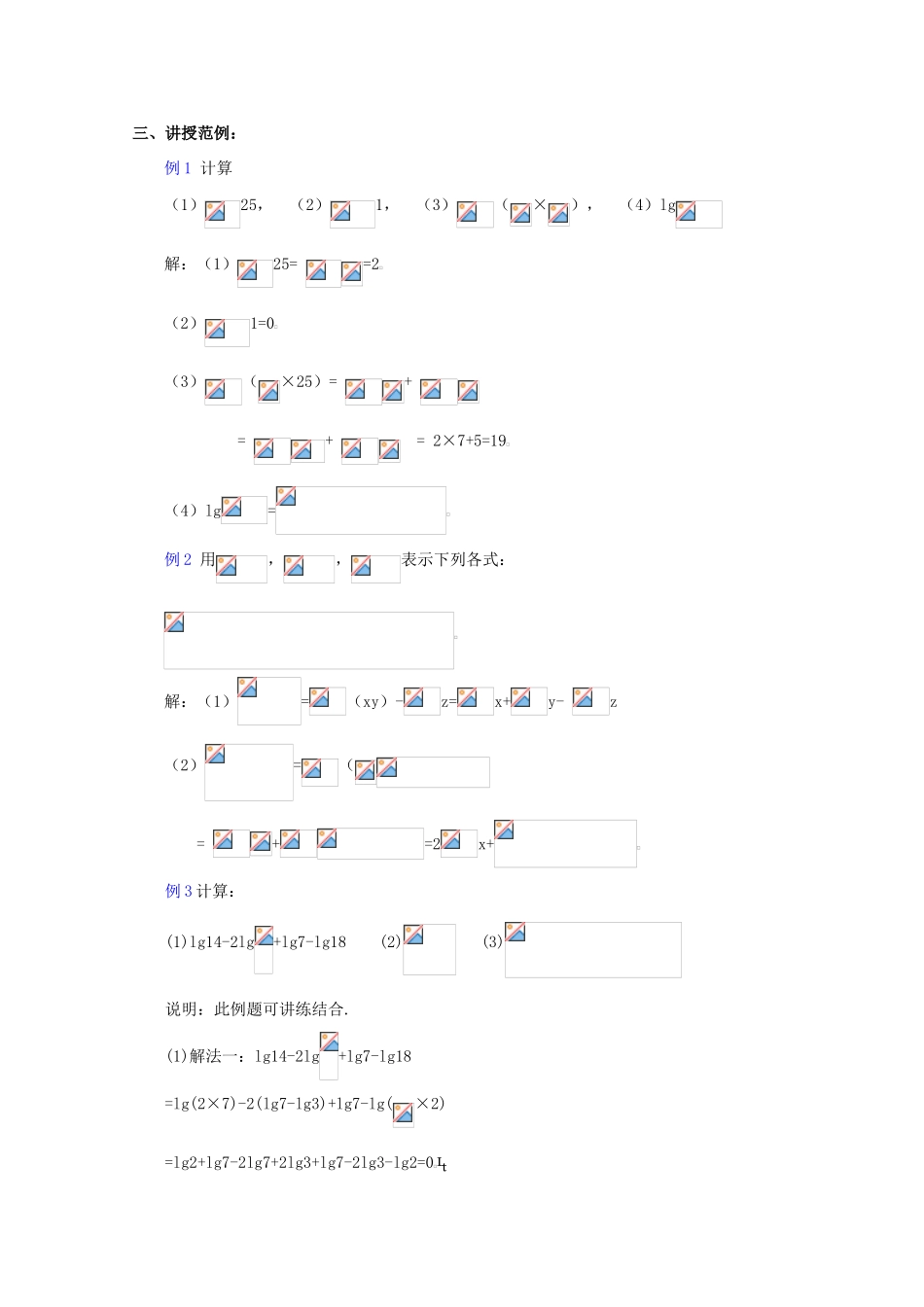
课 题:2.7.2 对数的运算性质教学目的: 1.掌握对数的运算性质,并能理解推导这些法则的依据和过程;2.能较熟练地运用法则解决问题;教学重点:对数运算性质教学难点:对数运算性质的证明方法.授课类型:新授课课时安排:1 课时教 具:多媒体、实物投影仪教学过程:一、复习引入:1.对数的定义 其中 a 与 N2.指数式与对数式的互化底数对数真数幂指数底数↓↓↓↓↓↓log a N=ba b =N3.重要公式:⑴ 负数与零没有对数;⑵,⑶ 对数恒等式3.指数运算法则 二、新授内容:积、商、幂的对数运算法则:如果 a > 0,a 1,M > 0, N > 0 有:证明:①设M=p, N=q由对数的定义可以得:M=,N=∴MN= = ∴MN=p+q,即证得MN=M + N② 设M=p,N=q由对数的定义可以得 M=,N= ∴ ∴即证得③ 设M=P 由对数定义可以得 M=,∴= ∴=np, 即证得=nM说明:上述证明是运用转化的思想,先通过假设,将对数式化成指数式,并利用幂的运算性质进行恒等变形;然后再根据对数定义将指数式化成对数式① 简易语言表达:“积的对数 = 对数的和”……② 有时逆向运用公式:如③ 真数的取值范围必须是: 是不成立的 是不成立的④ 对公式容易错误记忆,要特别注意: ,三、讲授范例:例 1 计算(1)25, (2)1, (3)(×), (4)lg解:(1)25= =2(2)1=0(3)(×25)= + = + = 2×7+5=19(4)lg=例 2 用,,表示下列各式:解:(1)=(xy)-z=x+y- z(2)=( = +=2x+例 3 计算:(1)lg14-2lg+lg7-lg18 (2) (3) 说明:此例题可讲练结合.(1)解法一:lg14-2lg+lg7-lg18=lg(2×7)-2(lg7-lg3)+lg7-lg(×2)=lg2+lg7-2lg7+2lg3+lg7-2lg3-lg2=0 解法二:lg14-2lg+lg7-lg18=lg14-lg+lg7-lg18=lg评述:此题体现了对数运算性质的灵活运用,运算性质的逆用常被学生所忽视.评述:此例题体现对数运算性质的综合运用,应注意掌握变形技巧,如 (3)题各部分变形要化到最简形式,同时注意分子、分母的联系.(2)题要避免错用对数运算性质.四、课堂练习:1.求下列各式的值:(1)6-3 (2)lg 5+lg 2(3)3+ (4)5-15解:(1)6-3=2=1(2)lg 5+lg 2=lg(5×2)=lg 10=1(3) 3+=(3×)=1=0(4) 5-15===-3=-1. 2. 用 lg x,lg y,lg z表示下列各式:(1) lg(xyz); (2)lg; (3); (4)解:(1) lg(xyz)=lg x+lg y+...