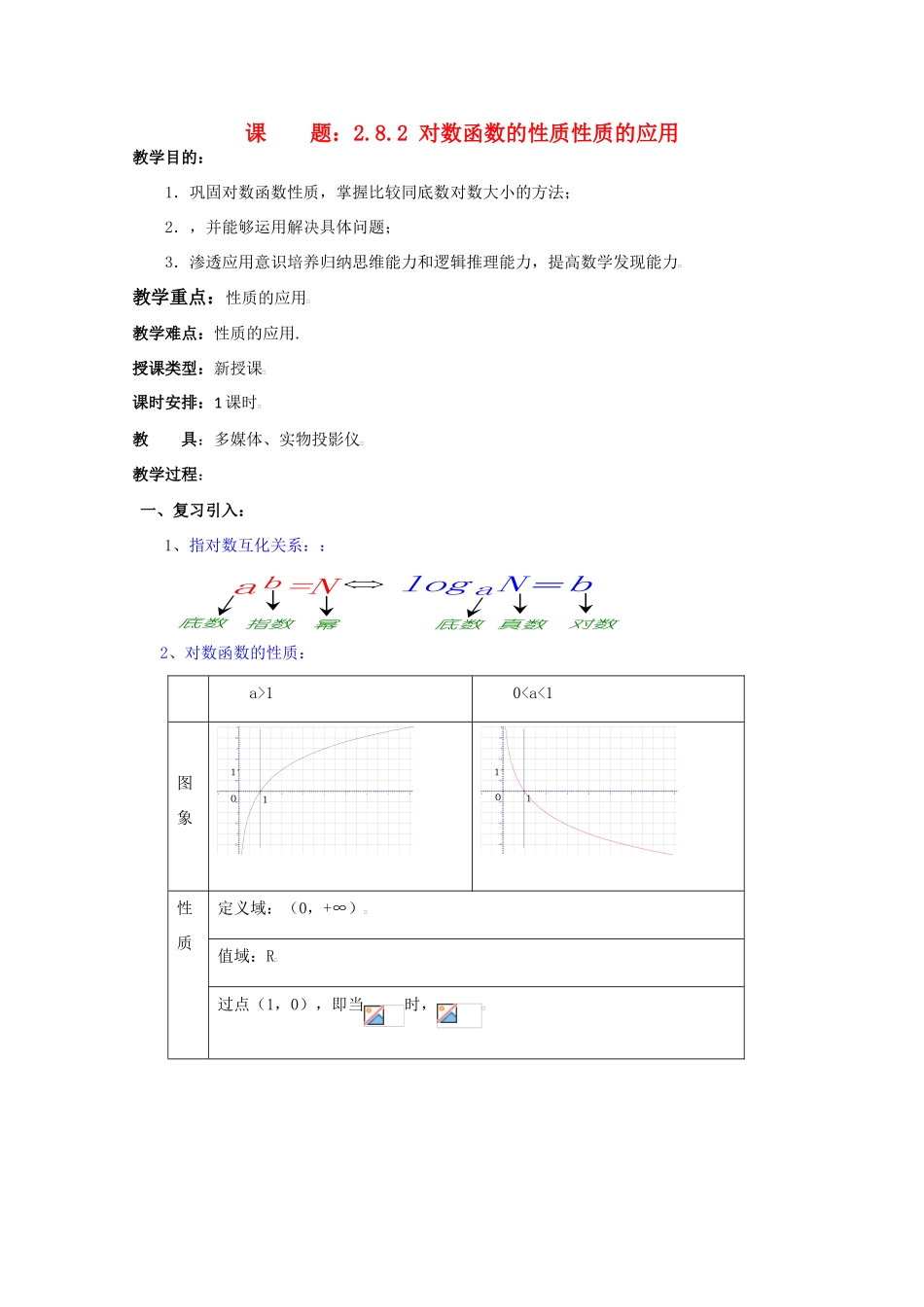
课 题:2.8.2 对数函数的性质性质的应用教学目的: 1.巩固对数函数性质,掌握比较同底数对数大小的方法;2.,并能够运用解决具体问题;3.渗透应用意识培养归纳思维能力和逻辑推理能力,提高数学发现能力 教学重点:性质的应用教学难点:性质的应用.授课类型:新授课课时安排:1 课时教 具:多媒体、实物投影仪教学过程: 一、复习引入:1、指对数互化关系::底数对数真数幂指数底数↓↓↓↓↓↓log a N=ba b =N2、对数函数的性质:a>10
1,所以它在(0,+∞)上是增函数,于是⑵ 考查对数函数,因为它的底数 0<0.3<1,所以它在(0,+∞)上是减函数,于是小结 1:两个同底数的对数比较大小的一般步骤: ① 确定所要考查的对数函数;② 根据对数底数判断对数函数增减性;③ 比较真数大小,然后利用对数函数的增减性判断两对数值的大小⑶ 当时,在(0,+∞)上是增函数,于是当时,在(0,+∞)上是减函数,于是小结 2:分类讨论的思想对数函数的单调性取决于对数的底数是大于 1 还是小于 1 而已知条件并未指明,因此需要对底数进行讨论,体现了分类讨论的思想,要求学生逐步掌握例 3 比较下列各组中两个值的大小:⑴; ⑵分析:由于两个对数值不同底,故不能直接比较大小,可在两对数值中间插入一个已知数,间接比较两对数的大小解:⑴,,⑵,,; 小结 3:引入中间变量比较大小例 3 仍是利用对数函数的增减性比较两个对数的大小,当不能直接比较时,经常在两个对数中间插入 1 或 0 等,间接比较两个对数的大小 例 4 求下列函数的定义域、值域:⑴ ⑵⑶ ⑷解:⑴要使函数有意义,则须: 即: ∴ 从而 ∴ ∴ ∴ ∴定义域为[-1,1],值域为⑵ 对一切实数都恒成立 ∴函数定义域为 R 从而 即函数值域为⑶ 要使函数有意义,则须: 由 ∴在此区间内 ∴ 从而 即:值域为 ∴定义域为[-1,5],值域为⑷ 要使函数有意义,则须:由①: 由②: 时 则须 , 综合①②得 当时 ∴ ∴ ∴ ∴定义域为(-1,0),值域为三、练习:比较大小⑴⑵⑶ 四、小结 本节课学习...