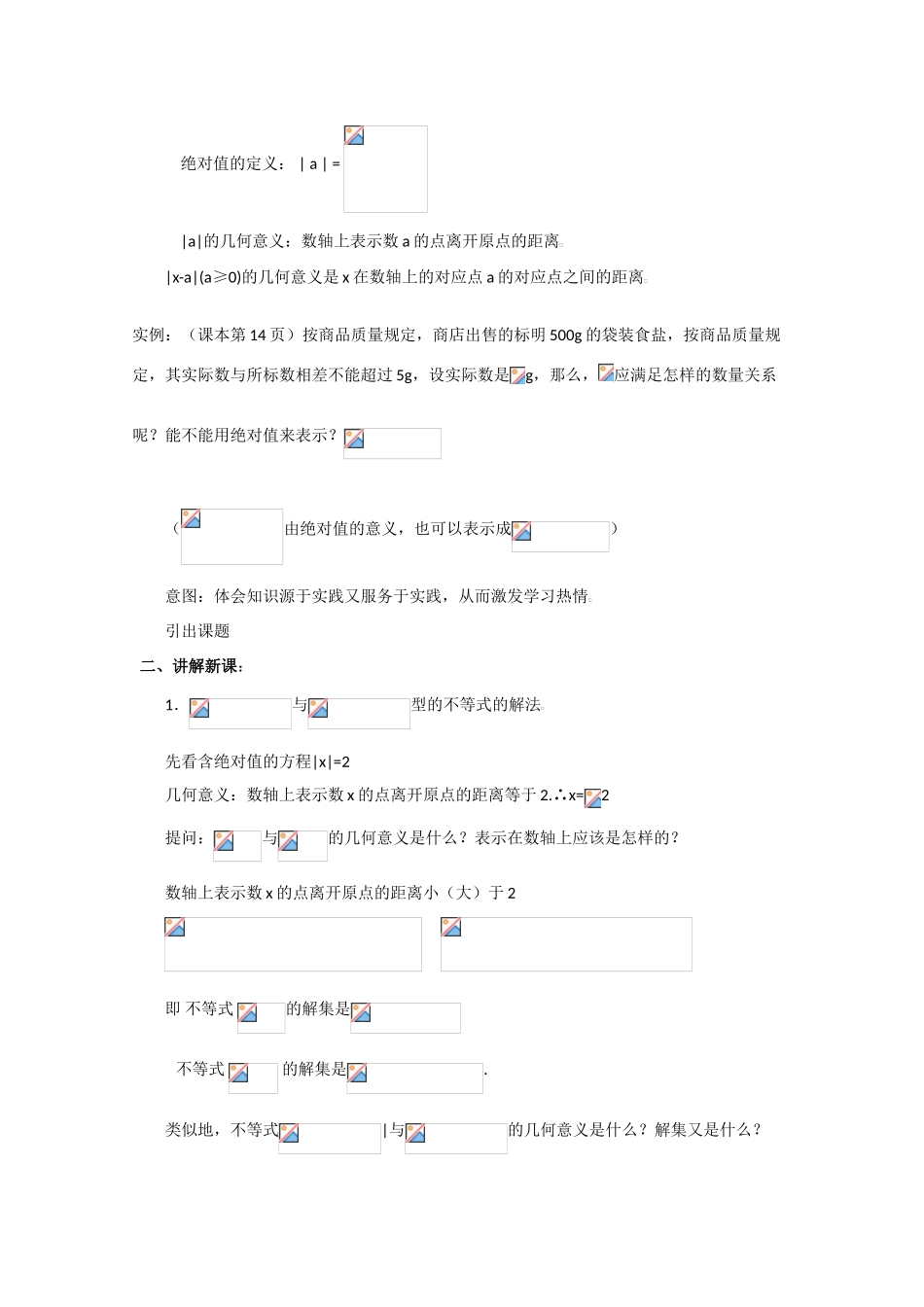
课 题:1.4 绝对值不等式的解法(1)教学目的:(1)理解并掌握与型不等式的解法,并能初步地应用它解决问题;(2)了解数形结合,分类讨论的思想,培养数形结合的能力,培养通过换元转化的思想方法,培养抽象思维的能力;(3)绝对值的几何意义的应用;(4)激发学习数学的热情,培养勇于探索的精神,勇于创新精神,同时体会事物之间普遍联系的辩证思想教学重点:与型不等式的解法教 学 难 点 : 绝 对 值 意 义 的 应 用 , 和 应 用与型 不 等 式 的 解 法 解 决与型不等式授课类型:新授课课时安排:1 课时教 具:多媒体、实物投影仪内容分析:(略) 教学过程: 一、复习引入:1.什么叫不等式?什么叫不等式组的解集?2.初中已学过的不等式的三条基本性质是什么?你能用汉语语言叙述这三条性质吗?1.如果 a>b,那么 a+c>b+c;2.如果 a>b,c>0,那么 ac > bc;3.如果 a>b,c<0,那么 ac < bc.3.实数的绝对值是如何定义的?几何意义是什么? 绝对值的定义: | a | = |a|的几何意义:数轴上表示数 a 的点离开原点的距离|x-a|(a≥0)的几何意义是 x 在数轴上的对应点 a 的对应点之间的距离实例:(课本第 14 页)按商品质量规定,商店出售的标明 500g 的袋装食盐,按商品质量规定,其实际数与所标数相差不能超过 5g,设实际数是g,那么,应满足怎样的数量关系呢?能不能用绝对值来表示?(由绝对值的意义,也可以表示成)意图:体会知识源于实践又服务于实践,从而激发学习热情引出课题 二、讲解新课:1.与型的不等式的解法先看含绝对值的方程|x|=2几何意义:数轴上表示数 x 的点离开原点的距离等于 2.∴x=2提问:与的几何意义是什么?表示在数轴上应该是怎样的?数轴上表示数 x 的点离开原点的距离小(大)于 2 即 不等式 的解集是 不等式 的解集是.类似地,不等式|与的几何意义是什么?解集又是什么?即 不等式的解集是; 不等式的解集是小结:①解法:利用绝对值几何意义 ②数形结合思想2.,与型的不等式的解法把 看作一个整体时,可化为与型的不等式来求解即 不等式的解集为 ; 不等式的解集为 三、讲解范例: 例 1(课本第 15 页)解不等式.解:由原不等式可得,各加上 500,得,∴原不等式的解集是.例 2(课本第 15 页)解不等式.解:由原不等式可得,或.整理,得,或.∴原不等式的解集是.例 3(课本第 16 页练习 2(3))解不等式.解:原不等式可化为,...