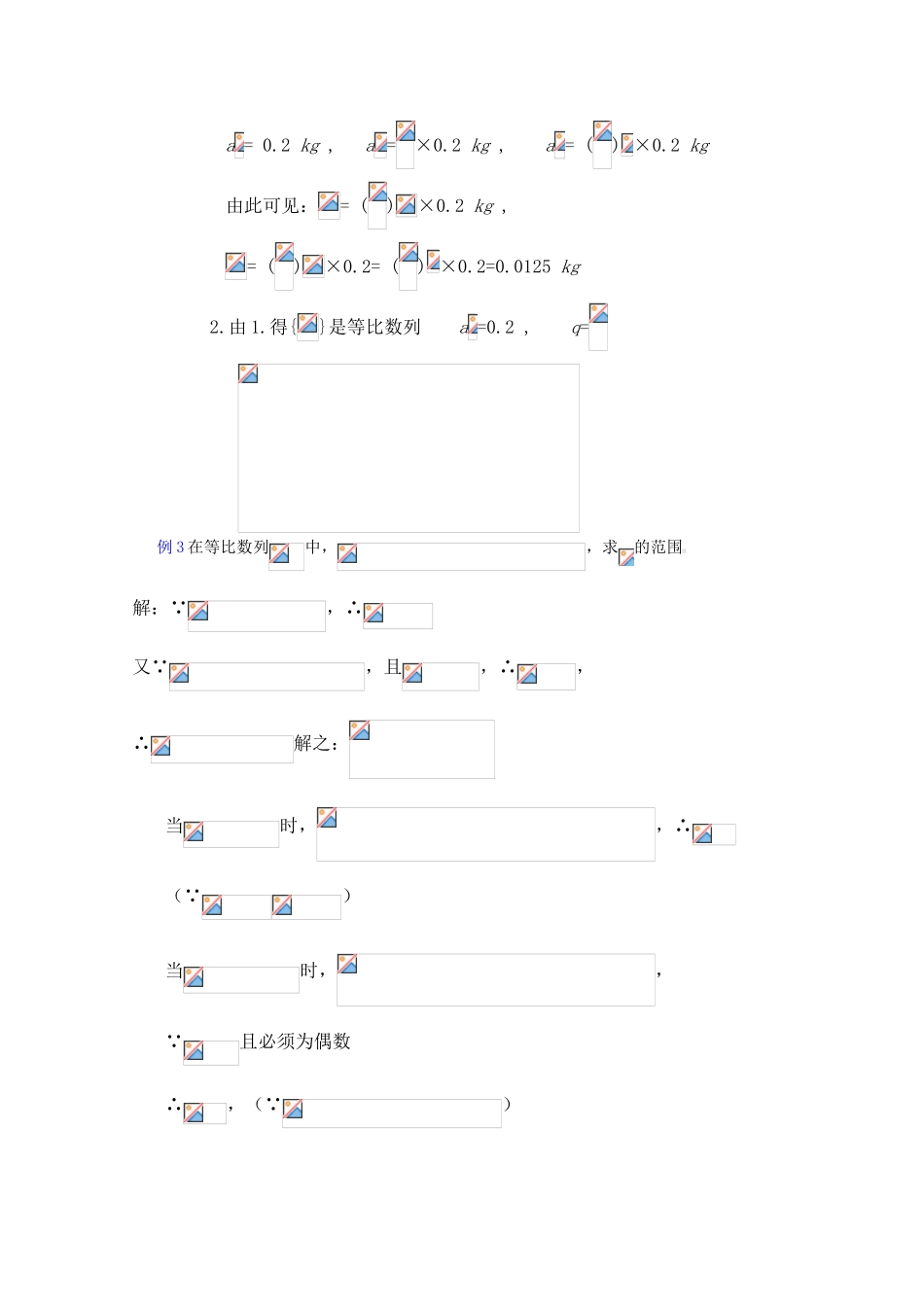
贵州省贵大附中 2011 届数学复习教学案:数列复习小结(2)教学目的:1.进一步掌握数列的有关概念和公式的应用2.要求学生对等差、等比数列有更深刻的理解,逐渐形成熟练技巧授课类型:复习课课时安排:1 课时教 具:多媒体、实物投影仪教学过程:一引入:上一节总结了数列的有关概念、方法、公式等,本节继续通过讲解例题,进一步加深和提高运用所学知识解决问题的灵活性 二、例题讲解例 1 在△ABC 中,三边成等差数列,也成等差数列,求证△ABC 为正三角形 证:由题设,且 ∴ ∴ 即 从而 ∴ (获证)例 2 从盛有盐的质量分数为 20%的盐水 2 kg 的容器中倒出 1 kg 盐水,然后加入 1 kg 水,以后每次都倒出 1 kg 盐水,然后再加入 1 kg 水,问:1.第 5 次倒出的的 1 kg 盐水中含盐多少 g? 2.经 6 次倒出后,一共倒出多少 k 盐?此时加 1 kg 水后容器内盐水的盐的质量分数为多少?解:1.每次倒出的盐的质量所成的数列为{},则: a = 0.2 kg , a =×0.2 kg , a = () ×0.2 kg 由此可见:= ()×0.2 kg , = ()×0.2= () ×0.2=0.0125 kg 2.由 1.得{}是等比数列 a =0.2 , q= 例 3 在等比数列中,,求的范围解: ,∴又 ,且,∴,∴解之:当时,,∴( )当时,, 且必须为偶数∴,( )例 4 设{}, {}都是等差数列,它们的前 n 项和分别为, , 已知,求⑴;⑵ ⑴ 解法 1:===.⑴ 解法 2: {}, {}都是等差数列∴可设=kn(5n+3), =kn(2n-1)∴=-= k[n(5n+3)-(n-1)(5(n-1)+3)]=kn(10n-2), =-=k[n(2n-1)-(n-1)(2(n-1)-1)] =kn(4n-3),∴==⑵ 解:由⑴解法 2,有=-= k[n(5n+3)-(n-1)(5(n-1)+3)]=kn(10n-2), =-=k[n(2n-1)-(n-1)(2(n-1)-1)] =kn(4n-3), ∴=k5(105-2)=240k =k8(48-3)=232k ∴ =例 5 设等差数列{}的前 n 项和为, (1)如果 a =9, S =40, 问是否存在常数 c,使数列{}成等差数列;(2)如 果= n - 6n, 问 是 否 存 在 常 数 c , 使 得=对任意自然数 n 都成立 解:(1) 由 a =9, S =40, 得 a =7, d=2, ∴ =2n+5, =n2+6n, = ∴ 当 c=9 时, =n+3 是等差数列; (2) =对任意自然数 n 都成立,等价于{}成等差数列, 由于=n -6n ∴=, 即使 c=9, =|n-3|, 也不会成等差数列,因此不存在这样的常数 c 使得=对任意自然数 n都成立三、课后作业:1....