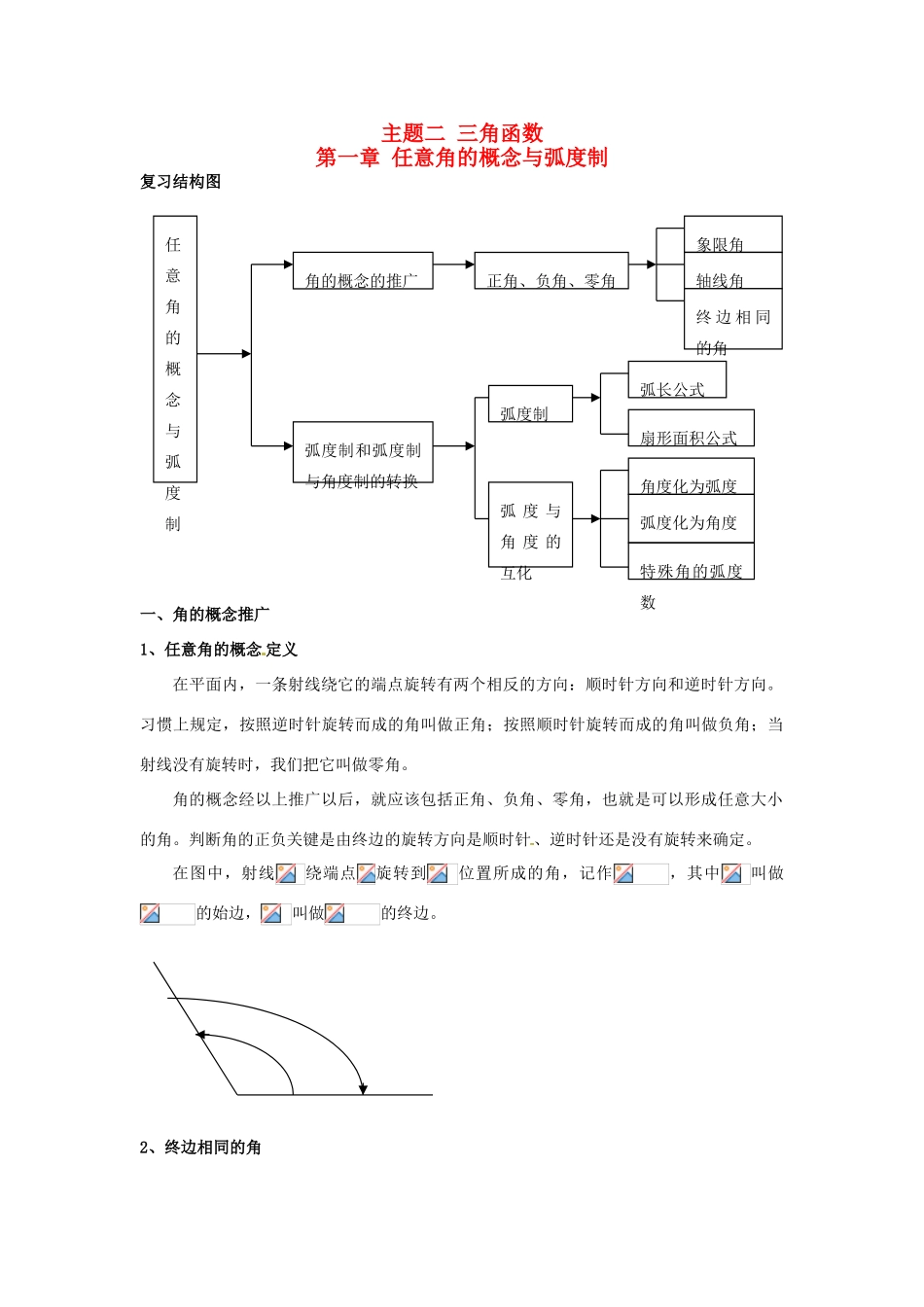
主题二 三角函数第一章 任意角的概念与弧度制复习结构图一、角的概念推广1、任意角的概念 定义在平面内,一条射线绕它的端点旋转有两个相反的方向:顺时针方向和逆时针方向。习惯上规定,按照逆时针旋转而成的角叫做正角;按照顺时针旋转而成的角叫做负角;当射线没有旋转时,我们把它叫做零角。角的概念经以上推广以后,就应该包括正角、负角、零角,也就是可以形成任意大小的角。判断角的正负关键是由终边的旋转方向是顺时针、逆时针还是没有旋转来确定。在图中,射线绕端点旋转到位置所成的角,记作,其中叫做的始边,叫做的终边。2、终边相同的角任意角的概念与弧度制角的概念的推广弧度制和弧度制与角度制的转换正角、负角、零角象限角轴线角终 边 相 同的角弧度制弧长公式扇形面积公式弧 度 与角 度 的互化角度化为弧度弧度化为角度特殊角的弧度数设表示任意角,所有与终边相同的角,包括本身构成一个集合,这个集合可记为。集合的每一个元素都与的终边相等,当时,对应元素为。相等的角终边一定相同,终边相同的角不一定相等,终边相同的角有无数个,它们相差的整数倍。例 1:在范围内,找出与角终边相同的角,并写出所有与终边相同的角的集合。例 2:①写出与终边相同的角的集合;② 把写成的形式。例 3:与角终边相同的角表示为( )A、 B、 C、 D、3、象限角与轴线角今后我们通常在平面直角坐标系内讨论角。在平面内任意一个角都可以通过移动,使角的顶点与坐标原点重合,角的始边与轴正半轴重合。这时,角的终边在第几象限,就把这个角叫做第几象限角,如果终边在坐标轴上,就认为这个角不属于任何象限。例 1:画出下列各角,并指出该角是第几象限角。① ②例 2:给出下列命题:① 角与角的终边相等;② 第二象限的角一定大于第一象限的角;③ 第二象限的角是钝角;④ 小于的角是锐角。其中正确的命题序号是 。4、各象限角的集合与轴线角的集合(1)象限角的集合第一象限角集合为第二象限角的集合为第三象限角的集合为第四象限角的集合为(2)轴线角的集合终边落在轴的非负半轴上,角的集合为终边落在轴的非正半轴上,角的集合为终边落在轴上,角的集合为终边落在轴的非负半轴上,角的集合为终边落在轴的非正半轴上,角的集合为终边落在轴上,角的集合为终边落在坐标轴上,角的集合为终边落在同一条直线上的角相差的整数倍,终边落在同一条射线上的角相差的整数倍。例 1:在直角坐标系中,判断下列各语句的...