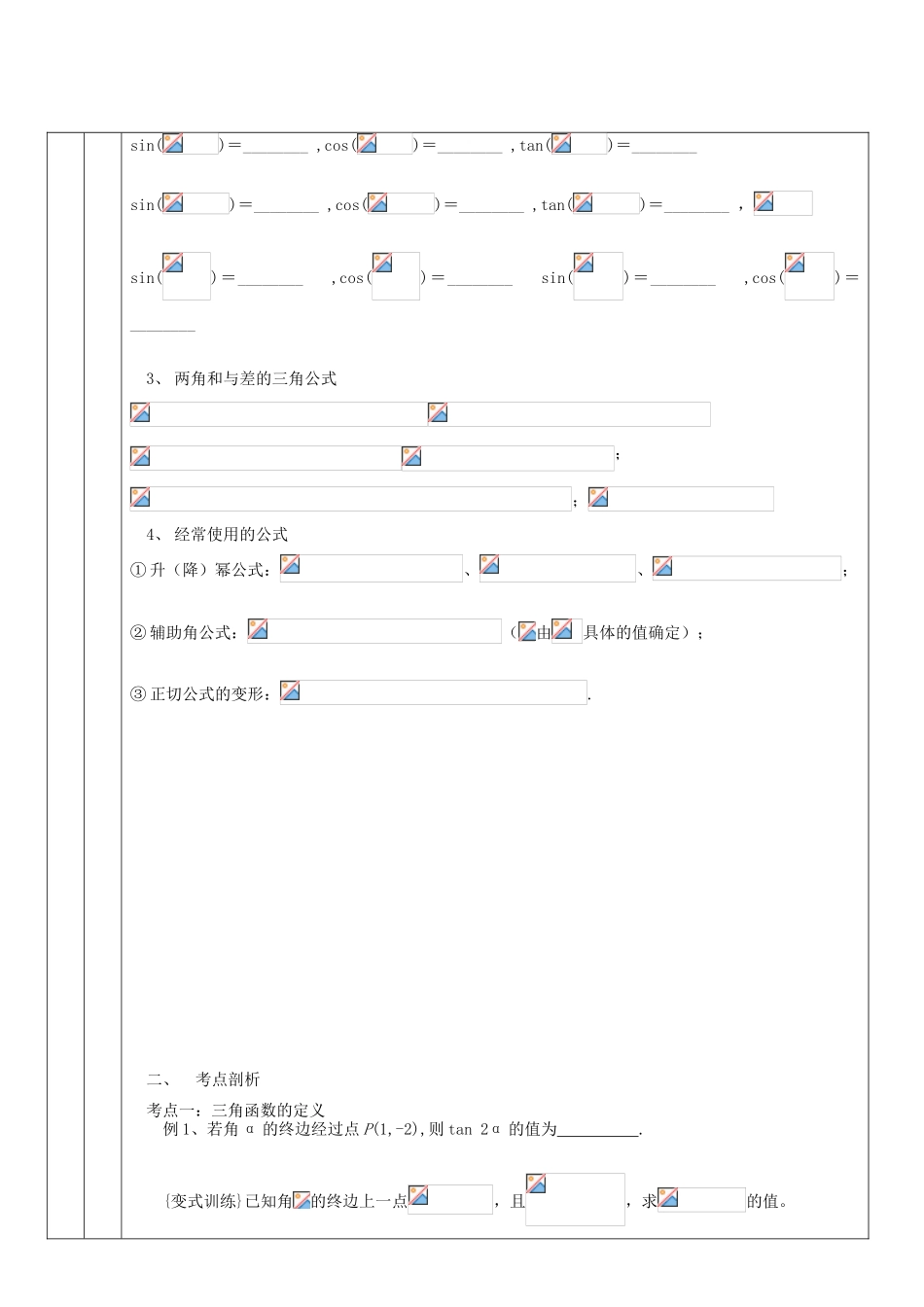
教 学内 容高三第一轮三角函数复习教案教 学目 标 自己填重 点难 点自己填教学过程课前检查与交流作业完成情况:交流与沟通针对性授课《三角函数》经典题型一、公式回顾1、 特殊角的三角函数值α02sinαcosαtanα2、 诱导公式sin()=_________,cos()=_________,tan()=__________sin()=_________,cos()=_________,,tan()=_________,sin()=_________ ,cos()=________ ,tan()=________ sin()=________ ,cos()=________ ,tan()=________ sin()=________ ,cos()=________ ,tan()=________ ,sin()=________ ,cos()=________ sin()=________ ,cos()=________ 3、 两角和与差的三角公式;;4、 经常使用的公式① 升(降)幂公式:、、;② 辅助角公式:(由具体的值确定);③ 正切公式的变形:.二、考点剖析考点一:三角函数的定义例 1、若角 α 的终边经过点 P(1,-2),则 tan 2α 的值为 .{变式训练}已知角的终边上一点,且,求的值。考点二:象限角例 2.若 sinθcosθ>0,则 θ 在( )A.第一、二象限 B.第一、三象限C.第一、四象限 D.第二、四象限 【变式训练 1】若 A、B 是锐角△ABC 的两个内角,则点 P(cosB-sinA,sinB-cosA)在( )A.第一象限 B.第二象限 C.第三象限 D.第四象限【变式训练 2】已知“是第三象限角,则是第__________象限角考点三:同角的三角函数关系1、 弦切互化例 3:(1)求值; (2)已知,求的值;2、 巧变“1”例 4:已知,求(Ⅰ);(Ⅱ)的值.考点四:“知一求二”例 5:(1)已知,,则___________ (2)若,则=___________(3)若 ,则 __ , 考点五:公式的双向应用例 6:(1)下列各式中,值为的是 ( ) A、 B、 C、 D、 ; (2) tan20°+tan40°+tan20°tan40°= (3)已知,那么的值为____ ;(4)的值是____ __;(5)若,,则 =____ 考点五:三角函数求值 1、给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“巧变角”,如等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;例 7:已知<α<,0<β<,cos(-α)=, sin(+β)=,求 sin(α+β)的值2、给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角. 例 8:(1)已知 α、β(,π)且 sinα=,β=,则 α+β= ,(2)已知,,已知均为锐角,则...