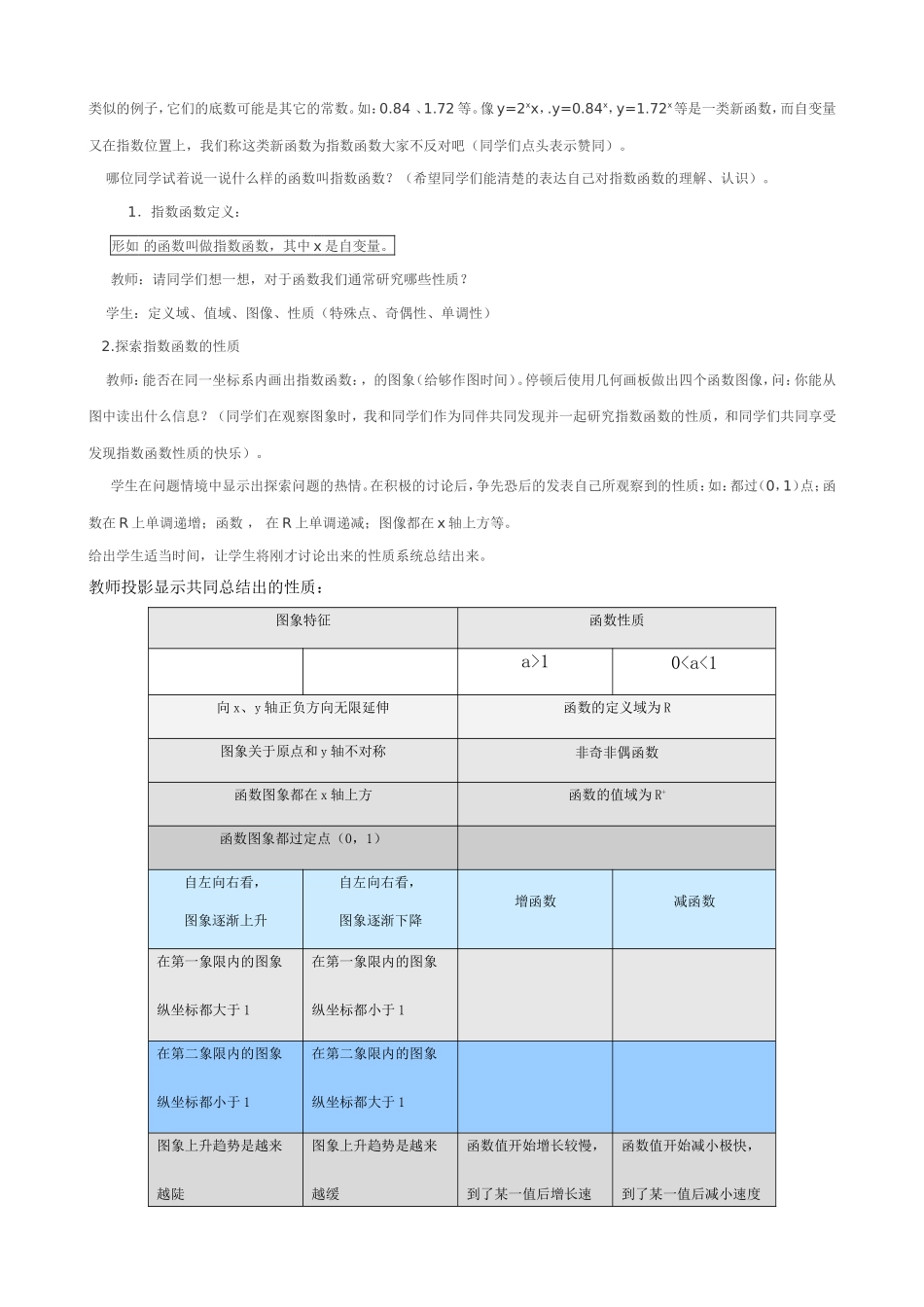
指数函数及其性质(第1课时)1.教学任务分析(1)使学生了解指数函数模型的实际背景,认识数学与现实生活、其他学科的联系.(2)理解指数函数的概念和意义,能画出具体指数函数的图象,探索并理解指数函数的单调性和特殊点.(3)在学习的过程中体会研究具体函数及其性质的过程和方法,如特殊到一般的过程、数形结合的方法等.2.教学重点和难点重点:指数函数的概念和性质.难点:用数形结合的方法从特殊到一般地探索、概括指数函数的性质.3.教学基本流程4.教学过程:一.创设情景,提出问题细胞分裂问题:某种细胞分裂时,第一次由1个分裂成2个,第二次由2个分裂成4个;第三次由4个分裂成8个,如此下去,如果第x次分裂得到y个细胞,那么细胞个数y与次数x的函数关系式是什么?学生:由问题的条件可知,细胞个数y与次数x的函数关系式是:y=2x(x∈N)。教师:都同意他的观点吗?(学生点头示意,表示赞同。此问句的目的是,给学习有困难的学生留有问问题的机会)。注:见机行事,追问:“x∈N”的实际意义是什么?(新课伊始,力求创设一种问题“场”,从实际问题进入,使学生感受到学习指数函数的必要性,同时也反映数学来源于实际)。二.师生共同学习,探求新知教师:在函数y=2x(x∈N)中,底数是常数,若指数是自变量,则幂值是指数的函数。其实在生活中我们还可以举出许多类似的例子,它们的底数可能是其它的常数。如:0.84、1.72等。像y=2xx,.y=0.84x,y=1.72x等是一类新函数,而自变量又在指数位置上,我们称这类新函数为指数函数大家不反对吧(同学们点头表示赞同)。哪位同学试着说一说什么样的函数叫指数函数?(希望同学们能清楚的表达自己对指数函数的理解、认识)。1.指数函数定义:形如的函数叫做指数函数,其中x是自变量。教师:请同学们想一想,对于函数我们通常研究哪些性质?学生:定义域、值域、图像、性质(特殊点、奇偶性、单调性)2.探索指数函数的性质教师:能否在同一坐标系内画出指数函数:,的图象(给够作图时间)。停顿后使用几何画板做出四个函数图像,问:你能从图中读出什么信息?(同学们在观察图象时,我和同学们作为同伴共同发现并一起研究指数函数的性质,和同学们共同享受发现指数函数性质的快乐)。学生在问题情境中显示出探索问题的热情。在积极的讨论后,争先恐后的发表自己所观察到的性质:如:都过(0,1)点;函数在R上单调递增;函数,在R上单调递减;图像都在x轴上方等。给出学生适当时间,让学生将刚才讨论出来的性质系统总结出来。教师投影显示共同总结出的性质:图象特征函数性质a>10