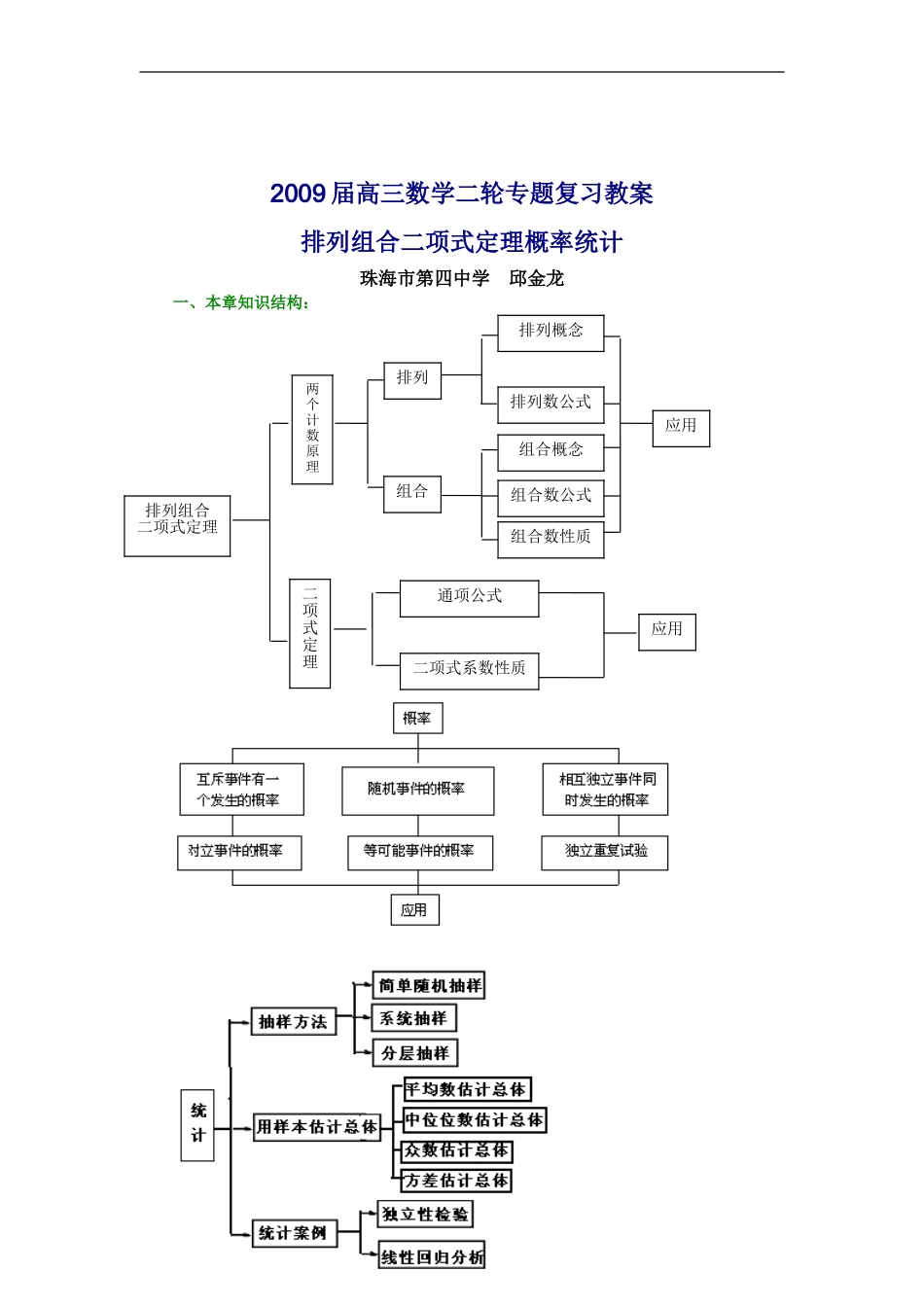
2009 届高三数学二轮专题复习教案排列组合二项式定理概率统计珠海市第四中学 邱金龙一、本章知识结构:用心 爱心 专心排列组合二项式定理两个计数原理排列组合排列概念排列数公式组合概念组合数公式组合数性质应用通项公式二项式定理二项式系数性质应用二、重点知识回顾1.排列与组合⑴ 分类计数原理与分步计数原理是关于计数的两个基本原理,两者的区别在于分步计数原理和分步有关,分类计数原理与分类有关.⑵ 排列与组合主要研究从一些不同元素中,任取部分或全部元素进行排列或组合,求共有多少种方法的问题.区别排列问题与组合问题要看是否与顺序有关,与顺序有关的属于排列问题,与顺序无关的属于组合问题.⑶ 排列与组合的主要公式① 排列数公式: (m≤n) A =n! =n(n―1)(n―2) ·…·2·1.② 组合数公式: (m≤n).③ 组合数性质:①(m≤n). ② ③2.二项式定理⑴ 二项式定理(a +b)n =C an +C an-1b+…+C an-rbr +…+C bn,其中各项系数就是组合数 C ,展开式共有 n+1 项,第 r+1 项是 Tr+1 =C an-rbr.⑵ 二项展开式的通项公式二项展开式的第 r+1 项 Tr+1=C an-rbr(r=0,1,…n)叫做二项展开式的通项公式。⑶ 二项式系数的性质① 在二项式展开式中,与首末两端“等距离”的两个二项式系数相等,即 C = C (r=0,1,2,…,n).② 若 n 是偶数,则中间项(第项)的二项公式系数最大,其值为 C ;若 n 是奇数,则中间两项(第项和第项)的二项式系数相等,并且最大,其值为 C= C.③ 所有二项式系数和等于 2n,即 C +C +C +…+C =2n.④ 奇数项的二项式系数和等于偶数项的二项式系数和,即 C +C +…=C +C +…=2n―1.3.概率用心 爱心 专心(1)事件与基本事件: 基本事件:试验中不能再分的最简单的“单位”随机事件;一次试验等可能的产生一个基本事件;任意两个基本事件都是互斥的;试验中的任意事件都可以用基本事件或其和的形式来表示. (2)频率与概率:随机事件的频率是指此事件发生的次数与试验总次数的比值.频率往往在概率附近摆动,且随着试验次数的不断增加而变化,摆动幅度会越来越小.随机事件的概率是一个常数,不随具体的实验次数的变化而变化. (3)互斥事件与对立事件: (4)古典概型与几何概型: 古典概型:具有“等可能发生的有限个基本事件”的概率模型. 几何概型:每个事件发生的概率只与构成事件区域的长度(面积或体积)成比例. 两种概型中每...