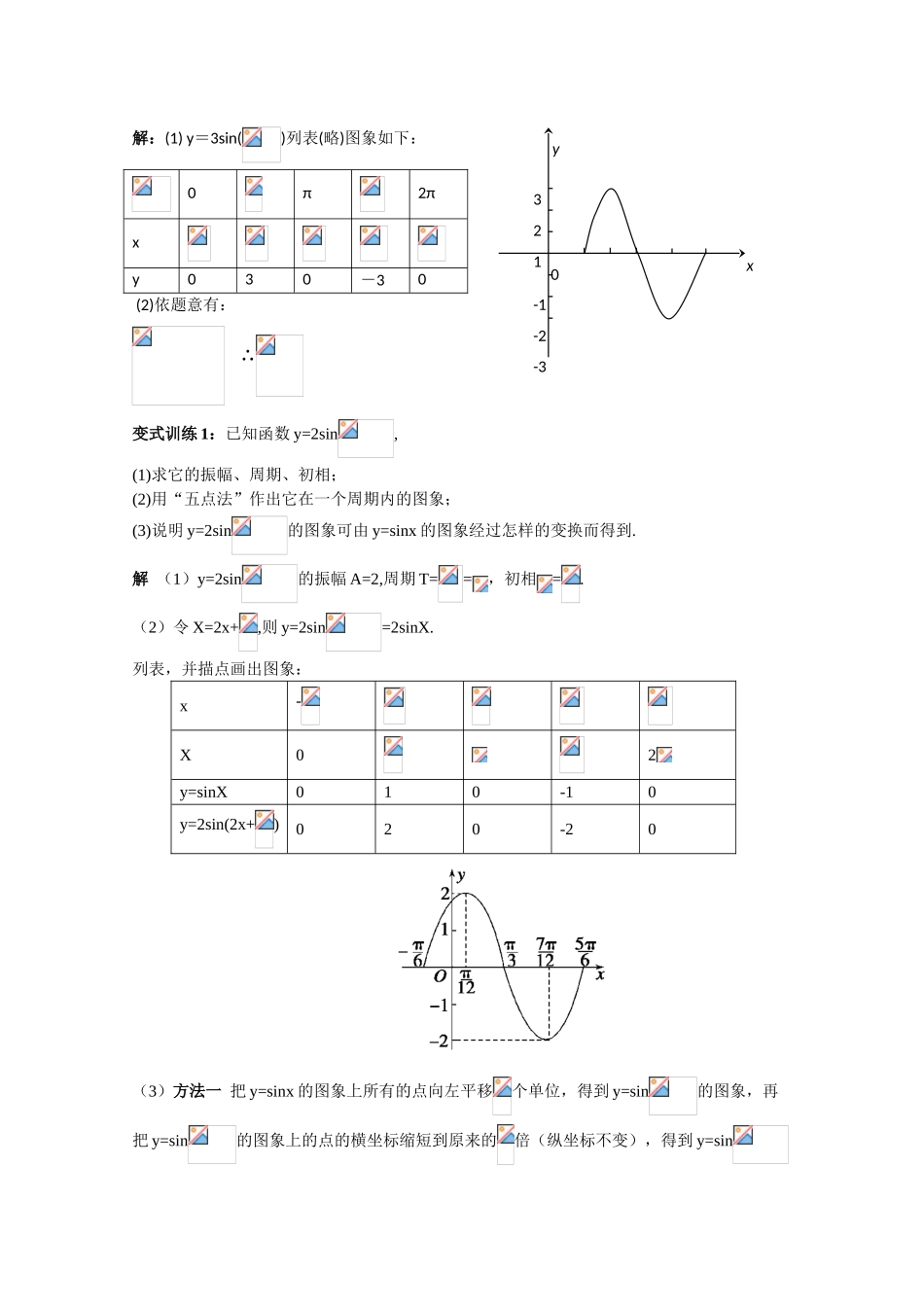
第 7 课时 三角函数的图象与性质1.用“五点法”作正弦、余弦函数的图象.“五点法”作图实质上是选取函数的一个 ,将其四等分,分别找到图象的 点, 点及“平衡点”.由这五个点大致确定函数的位置与形状.2.y=sinx,y=cosx,y=tanx 的图象.函数y=sinxy=cosxy=tanx图象注:⑴ 正弦函数的对称中心为 ,对称轴为 .⑵ 余弦函数的对称中心为 ,对称轴为 .⑶ 正切函数的对称中心为 .3.“五点法”作 y=Asin(ωx+)(ω>0)的图象.令 x'=ωx+转化为 y=sinx',作图象用五点法,通过列表、描点后作图象.4.函数 y=Asin(ωx+)的图象与函数 y=sinx 的图象关系.振幅变换:y=Asinx(A>0,A≠1)的图象,可以看做是 y=sinx 的图象上所有点的纵坐标都 ,(A>1)或 (0
0,ω≠1)的图象,可以看做是把 y=sinx 的图象上各点的横坐标 (ω>1)或 (0<ω<1)到原来的 倍(纵坐标不变)而得到的.由于 y=sinx 周期为 2π,故 y=sinωx(ω>0)的周期为 .相位变换:y=sin(x+)(≠0)的图象,可以看做是把 y=sinx 的图象上各点向 (>0)或向 (<0)平移 个单位而得到的.由 y=sinx 的图象得到 y=Asin(ωx+)的图象主要有下列两种方法:或说明:前一种方法第一步相位变换是向左(>0)或向右(<0)平移 个单位.后一种方法第二步相位变换是向左(>0)或向右(<0)平移 个单位.例 1.已知函数 y=Asin(ωx+)(A>0,ω>0)⑴ 若 A=3,ω=,=-,作出函数在一个周期内的简图.⑵ 若 y 表示一个振动量,其振动频率是,当 x=时,相位是,求 ω 和.基础过关y = sinx相位变换周期变换振幅变换y = sinx周期变换相位变换振幅变换解:(1) y=3sin()列表(略)图象如下:0π2πxy030-30 (2)依题意有: ∴变式训练 1:已知函数 y=2sin,(1)求它的振幅、周期、初相;(2)用“五点法”作出它在一个周期内的图象;(3)说明 y=2sin的图象可由 y=sinx 的图象经过怎样的变换而得到.解 (1)y=2sin的振幅 A=2,周期 T==,初相=.(2)令 X=2x+,则 y=2sin=2sinX.列表,并描点画出图象:x-X02y=sinX010-10y=2sin(2x+)020-20(3)方法一 把 y=sinx 的图象上所有的点向左平移个单位,得到 y=sin的图象,再把 y=sin的图象上的点的横坐标缩短到原来的倍(纵坐标不变),得到 y=sin321-1-2-3 xy0的图象,最后把 y=sin上所有点的纵坐标伸长到...