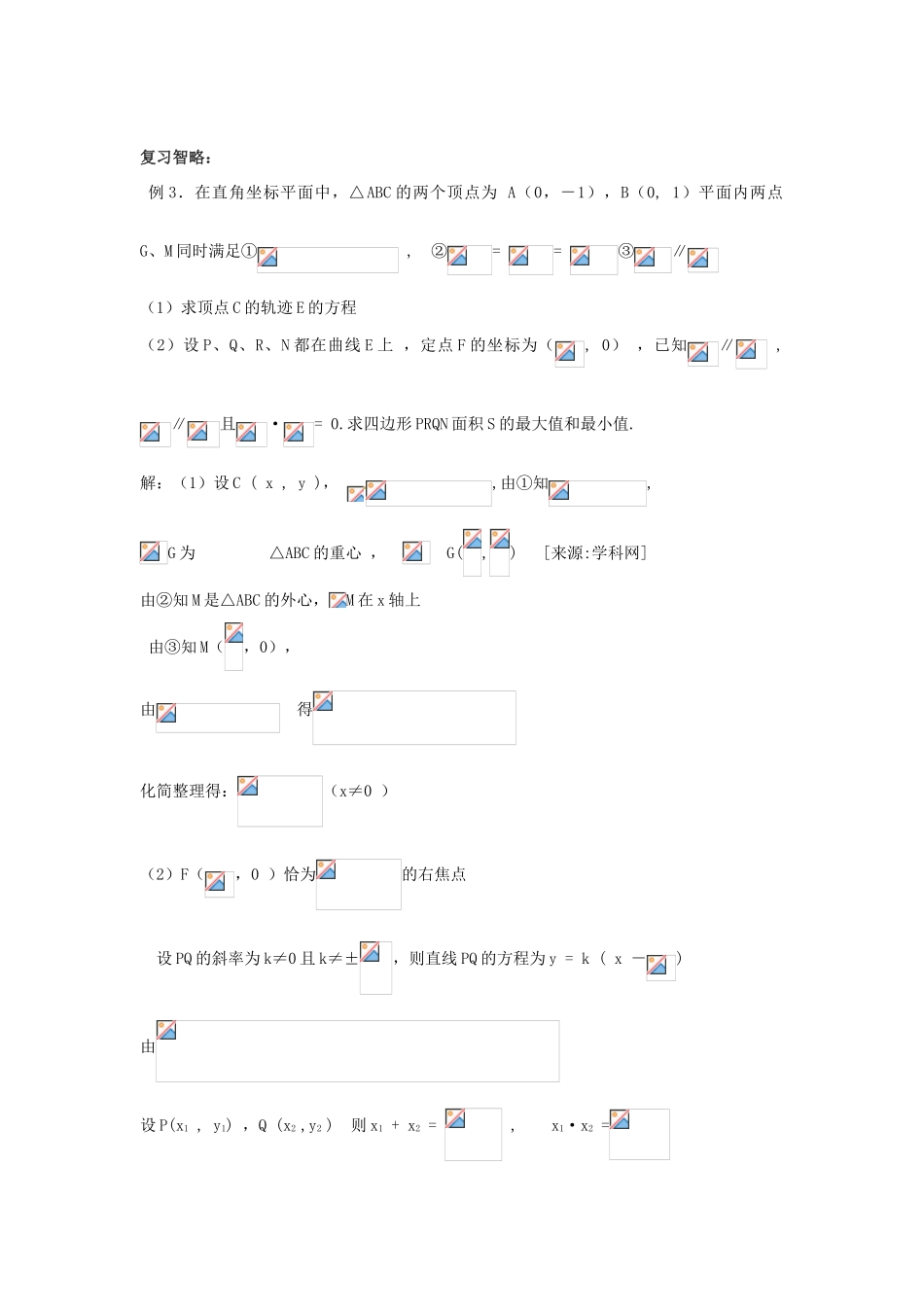
2011 年高考第二轮专题复习(教学案):平面向量考纲指要:重点考察向量的概念、向量的几何表示、向量的加减法、实数与向量的积、两个向量共线的充要条件、向量的坐标运算等。考点扫描:1.向量的概念:①向量;②零向量;③单位向量;④平行向量(共线向量);⑤相等向量。2.向量的运算:(1)向量加法;(2)向量的减法;(3)实数与向量的积。3.基本定理:(1)两个向量共线定理;(2)平面向量的基本定理。4.平面向量的坐标表示。5.向量的数量积:(1)两个非零向量的夹角;(2)数量积的概念;(3)数量积的几何意义;(4)向量数量积的性质;(5)两个向量的数量积的坐标运算;(6)垂直:如果与的夹角为 900则称与垂直,记作⊥。6.向量的应用:(1)向量在几何中的应用;(2)向量在物理中的应用。考题先知:例1.已 知 二 次 函 数 f ( x ) = x2 - 2x + 6 , 设 向 量 a = ( sinx , 2 ) , b = ( 2sinx ,) , [ 来源:Zxxk.Com]c=(cos2x,1),d=(1,2).当 x∈[0,π]时,不等式 f(a·b)>f(c·d)的解集为___________.[来源:学科网]解:a·b=2sin2x+1≥1, c·d=cos2x+1≥1,f(x)图象关于 x=1 对称,∴f(x)在(1,+∞)内单调递增.由 f(a·b)>f(c·d)a·b>c·d,即 2sin2x+1>2cos2x+1,又 x∈[0,π] ,∴x∈().故不等式的解集为().例 2.求函数的值域.分析:由于向 量沟通了代数与几何的内在联系,因此本题利用向量的有关知识求函数的值域。[来源:Z.xx.k.Com]解:因为,所以构造向量,,则,而,所以,得,另一方面:由,得,所以原函数的值域是.点评:在向量这部分内容的学习过程中,我们接触了不少含不等式结构的式子,如等。类比一:已知,求的最值。解:已知等式可化为,而,所以构造向量,则,从而最大值为 42,最小值为 8。 类比二:计算之值。解:构造单位圆的内接正五边形 ABCDE,使,,,,,则可证,从而原式=0类比三:已知实数满足,求证:。解:构造空间向量,即可。复习智略:例 3.在直角坐标平面中,△ABC 的两个顶点为 A(0,-1),B(0, 1)平面内两点G、M 同时满足① , ②= = ③∥ (1)求顶点 C 的轨迹 E 的方程(2)设 P、Q、R、N 都在曲线 E 上 ,定点 F 的坐标为(, 0) ,已知∥ , ∥且·= 0.求四边形 PRQN 面积 S 的最大值和最小值.解:(1)设 C ( x , y ), ,由①知,G 为...