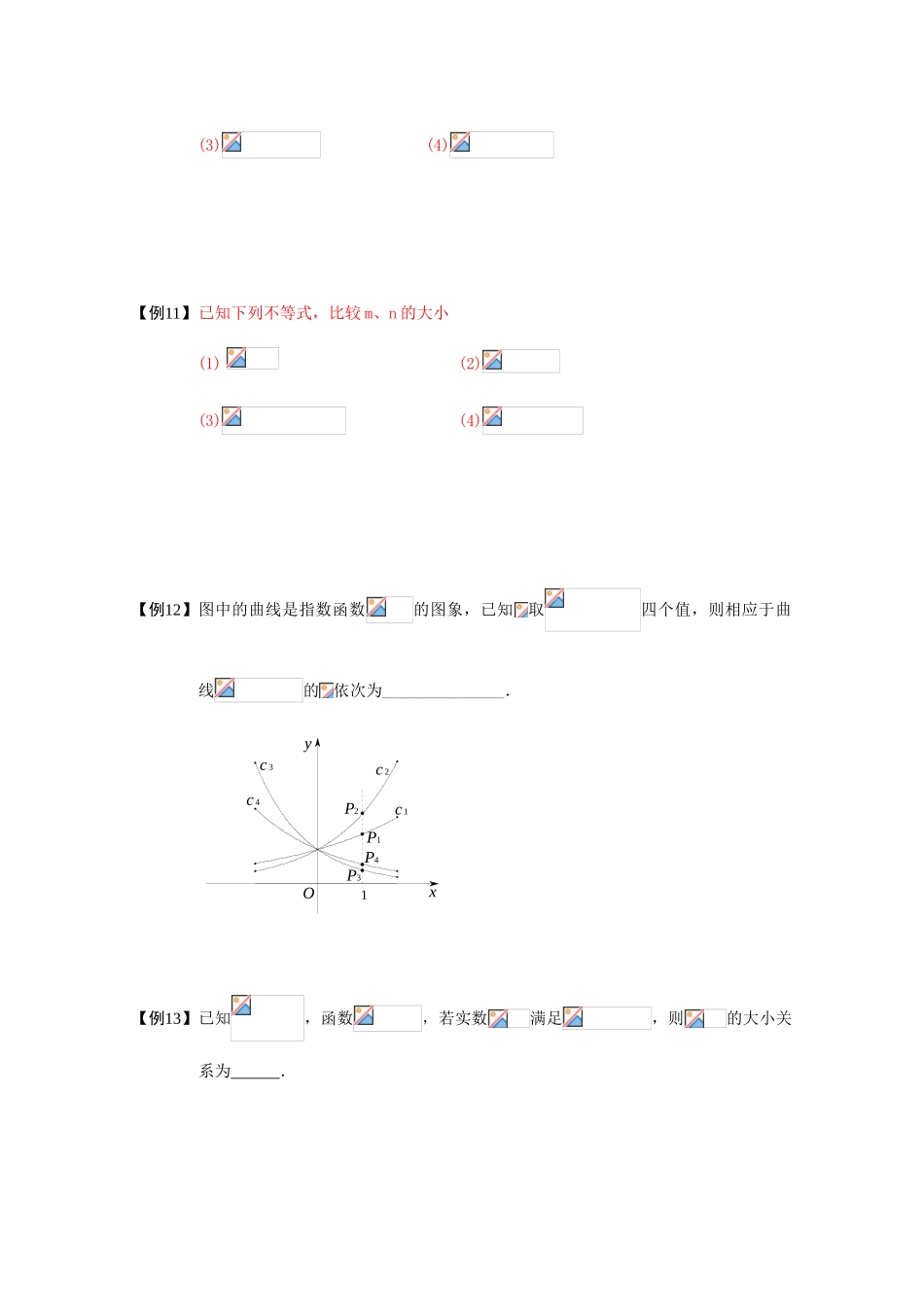
典例分析题型一 指数函数的定义与表示【例1】 求下列函数的定义域(1) (2)(3)(4) 【例2】 求下列函数的定义域、值域⑴ ; ⑵; ⑶【例3】 求下列函数的定义域和值域: 1. 2.【例4】 求下列函数的定义域、值域(1);(2).(3)板块二 . 指数函数【例5】 求下列函数的定义域(1);(2).【例6】 已 知 指 数 函 数且的 图 象 经 过 点, 求,,的值.【例7】 若,,且,则的值为( )A. B.或 C. D. 题型二 指数函数的图象与性质【例8】 已知,比较下列各组数的大小:①;② ;③;④.【例9】 比较下列各题中两个值的大小:⑴ ,;⑵ ,;⑶ ,.【例10】比较下列各题中两个值的大小(1)(2)(3)(4)【例11】已知下列不等式,比较 m、n 的大小(1) (2)(3)(4)【例12】图中的曲线是指数函数的图象,已知取四个值,则相应于曲线的依次为_______________.c 4c 3c 2c 1P4P3P2P11Oyx【例13】已知,函数,若实数满足,则的大小关系为 .【例14】设,,,则,,的大小关系是 【例15】若对,不等式恒成立,求实数的取值范围.【例16】判断函数的单调性.【例17】函数( )A.是奇函数,在上是减函数 B.是偶函数,在上是减函数C.是奇函数,在上是增函数 D.是偶函数,在上是增函数【例18】已知函数 f(x)为偶函数,当时,,求当时,的解析式.【例19】证明函数和 的图象关于 y 轴对称。题型三 关于指数的复合函数1.二次函数复合型【例20】求函数单调区间,并证明【例21】函数的单调增区间为 ,值域为 .【例22】函数,求在上的最小值.【例23】求函数 的值域.【例24】已知,当其值域为时,的取值范围是 【例25】求下列函数的单调区间.⑴(,且);⑵ 已知,求函数最值.【例26】函数的单调增区间是 .【例27】设,当时,的图象在轴上方,求的取值范围.【例28】如果函数在区间上的最大值是,求的值.【例29】求函数的单调区间及其值域.【例30】已知,求函数的最大值和最小值.【例31】求函数的最小值,并指出使取得最小值时的值2.分式函数复合型【例32】当 a>1 时,证明函数是奇函数.【例33】求证下列命题:(1)(a>0,a≠1)是奇函数;(2)(a>0,a≠1)是偶函数.【例34】已知函数,(1)判断函数的奇偶性;(2)求证函数在上是增函数.【例35】讨论函数的奇偶性、单调性,并求它的值域.【例36】已知,判断函数的单调性、奇偶性,并求的值域.【例37】正实数及函数满足,且,求的最小值【例38】设,...