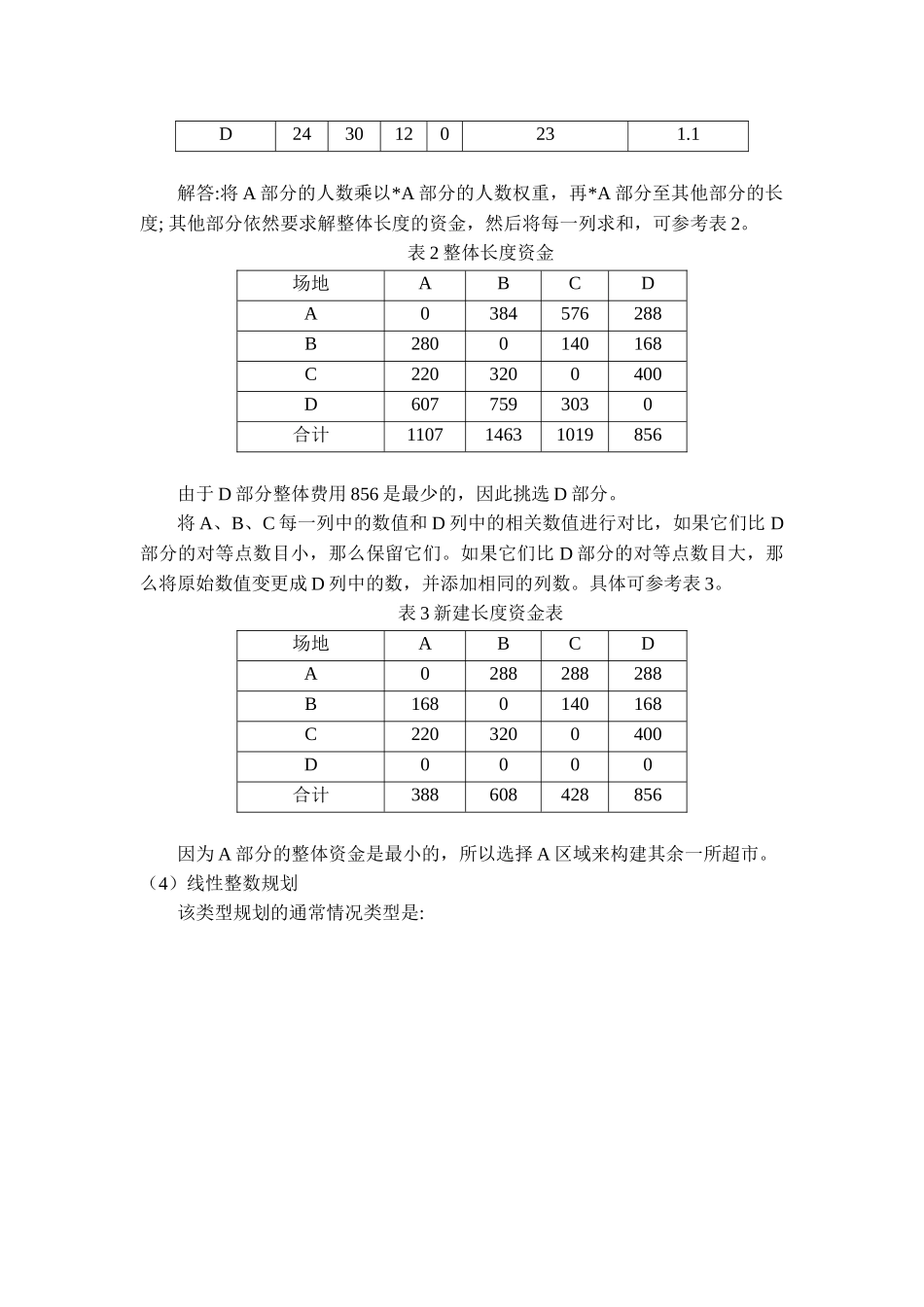
1.1选址相关理论分析选址分析作为一门应用广泛的技术,多年来,国内外相关专家学者做了大量的研究,也取得了丰硕的成果,一般而言,我们将选址分析方法分成两类:定量分析方法和定性分析方法。1.1.1定量分析方法数目分析途径通常情况采用描述资金的可量化数学公式来优化目标函数的方位。它的目的通常是尽量减少货物配送过程的总资金。利用调整若干参数和因变值,并对题目完成一系列的预想,它比利用求解模型可以知道解的简单模型更实用。更典型的数目分析途径包括重心法,物流作业量法、启发式算法、线性整数规划等。(1)重心法存在一系列我们可以把它看作制造量和需求位置的地方,每一个地方都有一系列数目的产品要运往贮存场所,以一系列的传送速率判断,或从贮存场所发出。贮存场所在哪里?我们将此点的运输成本比例乘以此点的运输成本比例,再乘以到此点的长度,就可以知道了上面我们所提到的货物相加总和(也就是总传送资金)极小值的点。那就是,在上述公式里我们可把TC看作是整体运输所需投入的资金把Vi看作是i点部分的运输数量把Ri看作是到达i点的运输费率把di看作是仓库至i点的长度通过下面两个公式,能够获得工厂所处方位。它的准确中点数值是和式中—位置待定的仓库的坐标Xi,Yi—产地和需求地的坐标距离di可以由下式估计得到式中,K我们可以把它看作一项测量因素,把坐标系上的一系列相关因素转换为更普遍的长度测距单位。(2)物流作业量法此途径求解每个收货地点的货物配送周转率,选择一个极小值用来当作最佳的收货地点,计算流程如下:i.调整坐标系。设a为要选择的新场地,b、c、d为新场地的关联方,也就是新场地物资供应点/货物交付点,每个点的坐标值都设置在此点附近。ii.求解新收货地点与关联方之间的长度。a与b的直线长度为:i.新站点与相关方在一系列时间内发生的货物配送业务量Q的统计。ii.求解新场地的货物配送量L。在上述公式里,我们把Qi看作是新站点和第i个有关站点的业务工作数量;我们把Di看作是新站点和第i个有关站点的长度;我们把n看作是有关站点的个数。iii.分别求解不一样新站点的业务作业量,在这当中地址的最小数值可看作是最佳的新址。(3)启发式方法若服务体系想在某一部分构建多个销售场所,并从极小值资金或整体长度的角度挑选销售场所的收货地点,那么能够使用启发类型的途径。一家连锁类型的整体企业打算在一个城市开两所超市。这个城市一共有4个部分,即A、B、C以及D,每个区去超市的人数的权重可参考表格2。那么这2所超市需要构建在这4个部分中的哪里?表1各区距离和人数权重区名距离各区人口(千人)人数权重ABCDA0203015161.2B2001012101.4C1116020201.0D2430120231.1解答:将A部分的人数乘以*A部分的人数权重,再*A部分至其他部分的长度;其他部分依然要求解整体长度的资金,然后将每一列求和,可参考表2。表2整体长度资金场地ABCDA0384576288B2800140168C2203200400D6077593030合计110714631019856由于D部分整体费用856是最少的,因此挑选D部分。将A、B、C每一列中的数值和D列中的相关数值进行对比,如果它们比D部分的对等点数目小,那么保留它们。如果它们比D部分的对等点数目大,那么将原始数值变更成D列中的数,并添加相同的列数。具体可参考表3。表3新建长度资金表场地ABCDA0288288288B1680140168C2203200400D0000合计388608428856因为A部分的整体资金是最小的,所以选择A区域来构建其余一所超市。(4)线性整数规划该类型规划的通常情况类型是:线性整数通常可以被分为以下3种:倘若全部的因变值均被看作限制整数,那么就把它叫做integerprogramming;倘若只有若干因变值属于该范畴,那么就把它叫做混合类型的integerprogramming。该模式下的一种非常规模式为0-1规划,它的因变值被限制为0或1该类型规划在integerprogramming中至关重要。与此同时,由于多数实际题目,如赋值题目,土地选择题目,发送产品等题目都能够归因于这样的模式。例:某公司计划在m个地点建厂,可供选择的地点有A1,A2…Am,他们的生产能力分别是a1,a2,…am(假设生产同一产品)。第i个工厂的建设费用为fi(i=1.2…m),又有n个地点B1,B2,…Bn需要销售这种产品,其销量分别...