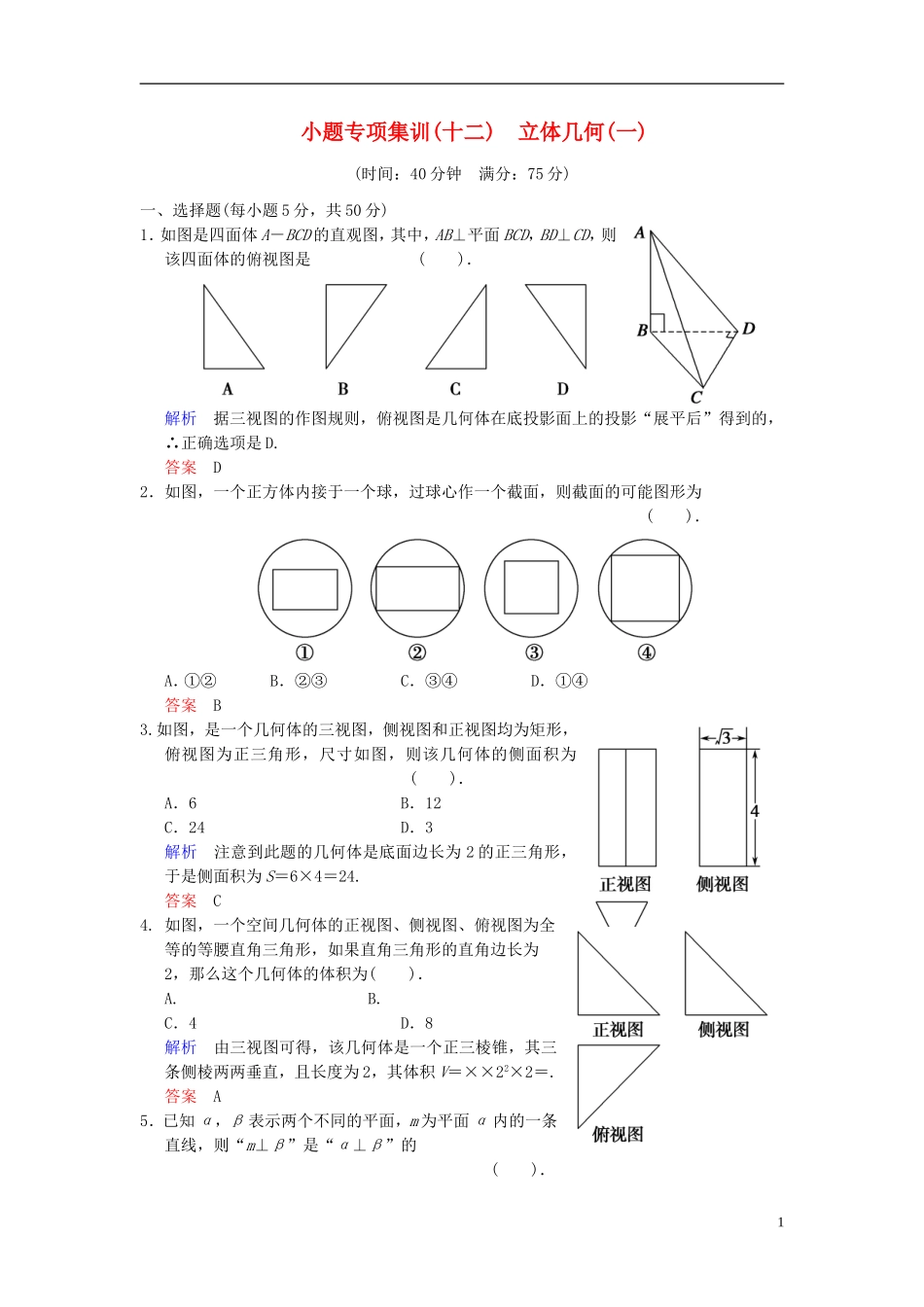
小题专项集训(十二) 立体几何(一)(时间:40 分钟 满分:75 分)一、选择题(每小题 5 分,共 50 分)1.如图是四面体 A-BCD 的直观图,其中,AB⊥平面 BCD,BD⊥CD,则该四面体的俯视图是 ( ). 解析 据三视图的作图规则,俯视图是几何体在底投影面上的投影“展平后”得到的,∴正确选项是 D.答案 D2.如图,一个正方体内接于一个球,过球心作一个截面,则截面的可能图形为 ( ).A.①② B.②③ C.③④ D.①④答案 B3.如图,是一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的侧面积为 ( ).A.6 B.12C.24 D.3解析 注意到此题的几何体是底面边长为 2 的正三角形,于是侧面积为 S=6×4=24.答案 C4. 如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为2,那么这个几何体的体积为( ).A. B. C.4 D.8解析 由三视图可得,该几何体是一个正三棱锥,其三条侧棱两两垂直,且长度为 2,其体积 V=××22×2=.答案 A5.已知 α,β 表示两个不同的平面,m 为平面 α 内的一条直线,则“m⊥β”是“α⊥β”的 ( ).1A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件解析 从两个方面分别判断.若 m⊂α,m⊥β,由面面垂直的判定定理知必有 α⊥β,所以充分性成立;反之,若直线 m⊂α,α⊥β,则直线 m 与平面 β 可以平行,也可以相交,所以必要性不成立,即在 m⊂α 的前提下,m⊥β 是 α⊥β 成立的充分不必要条件.答案 A6.给出下列四个命题:① 分别与两条异面直线都相交的两条直线一定是异面直线;② 若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③ 垂直于同一直线的两条直线相互平行;④ 若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中为真命题的是 ( ).A.①和② B.②和③ C.③和④ D.②和④解析 分别与两条异面直线都相交的两条直线可以是相交直线也可以是异面直线,即命题①不正确;若一个平面经过另一个平面的垂线,那么这两个平面相互垂直,即命题②正确;垂直于同一直线的两条直线相互平行或异面或相交,即命题③不正确;命题④正确,综上可得真命题的序号为②和④,故应选 D.答案 D7.设 a,b 是两条不同的直线,α,β 是两个不同的平面,则下列四个命题:① 若 a⊥b...