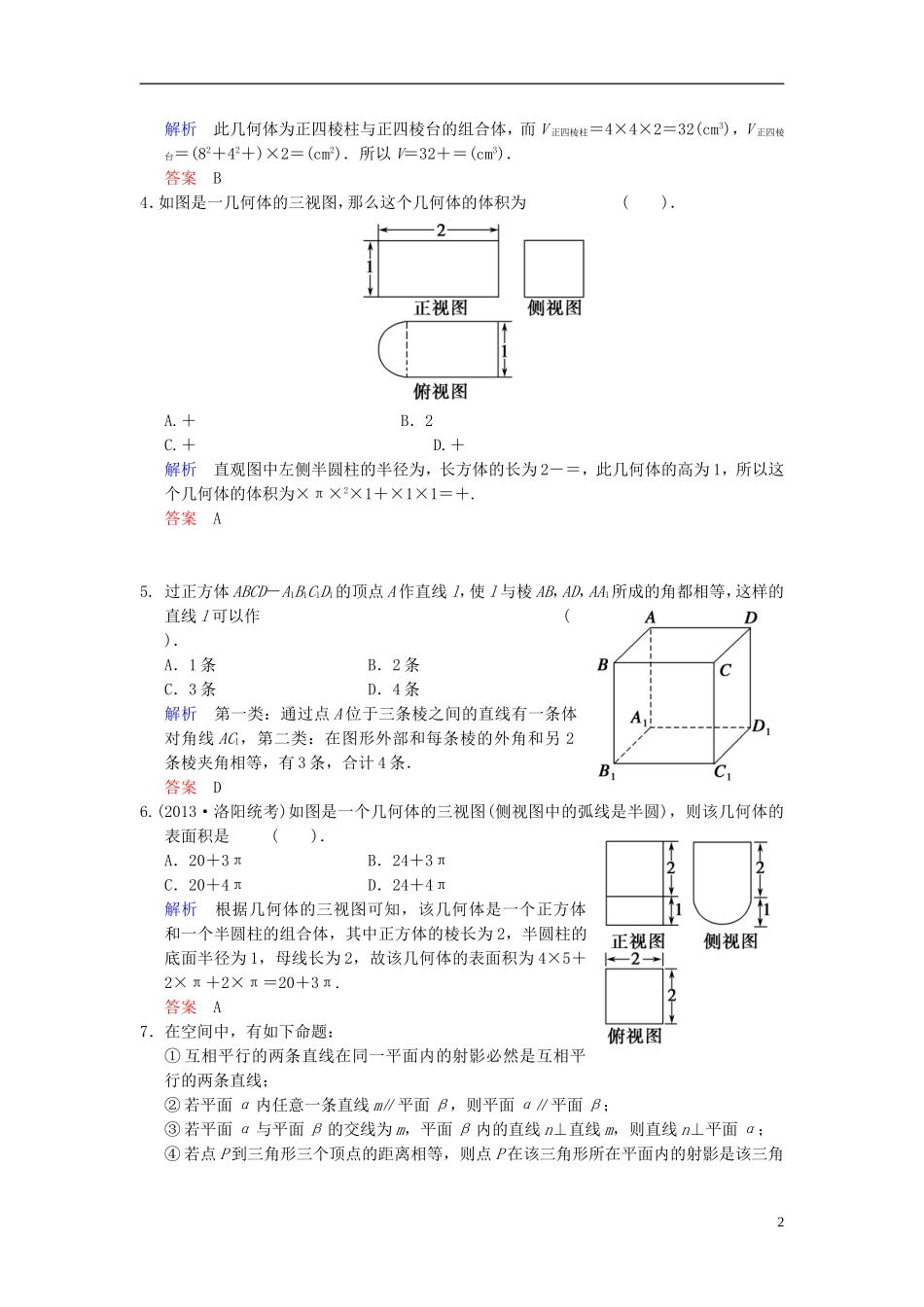
易失分点清零(九) 立体几何(一)1.在一个几何体的三视图中,正视图和俯视图如图,则相应的侧视图可以为 ( ).解析 由几何体的正视图和俯视图可知,该几何体的底面为半圆和等腰三角形,其侧视图可以是一个由等腰三角形及底边上的高构成的平面图形(实际上,此几何体为一个半圆锥和一个三棱锥的组合体),故应选 D.答案 D2.已知 m,n 是两条不同的直线,α,β 是两个不同的平面,有下列四个命题:① 若 m∥n,n⊂α,则 m∥α;② 若 m⊥n,m⊥α,n⊄α,则 n∥α;③ 若 α⊥β,m⊥α,n⊥β,则 m⊥n;④ 若 m,n 是异面直线,m⊂α,n⊂β,m∥β,则 n∥α.其中正确的命题有 ( ).A.①② B.②③ C.③④ D.②④解析 对于①,m 有可能也在 α 上,因此命题不成立;对于②,过直线 n 作垂直于 m 的平面 β,由 m⊥α,n⊄α 可知 β 与 α 平行,于是必有 n 与 α 平行,因此命题成立;对于③,由条件易知 m 平行于 β 或在 β 上,n 平行于 α 或在 α 上,因此必有 m⊥n;对于④,取正方体中两异面的棱及分别经过此两棱的不平行的正方体的两个面即可判断命题不成立.综上可知选 B.答案 B3.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是 ( ).A. cm3 B. cm3 C. cm3 D. cm31解析 此几何体为正四棱柱与正四棱台的组合体,而 V 正四棱柱=4×4×2=32(cm3),V 正四棱台=(82+42+)×2=(cm2).所以 V=32+=(cm3).答案 B4.如图是一几何体的三视图,那么这个几何体的体积为 ( ).A.+ B.2C.+ D.+解析 直观图中左侧半圆柱的半径为,长方体的长为 2-=,此几何体的高为 1,所以这个几何体的体积为×π×2×1+×1×1=+.答案 A5. 过正方体 ABCD-A1B1C1D1的顶点 A 作直线 l,使 l 与棱 AB,AD,AA1所成的角都相等,这样的直线 l 可以作 ( ).A.1 条 B.2 条C.3 条 D.4 条解析 第一类:通过点 A 位于三条棱之间的直线有一条体对角线 AC1,第二类:在图形外部和每条棱的外角和另 2条棱夹角相等,有 3 条,合计 4 条.答案 D6.(2013·洛阳统考)如图是一个几何体的三视图(侧视图中的弧线是半圆),则该几何体的表面积是 ( ).A.20+3π B.24+3πC.20+4π D.24+4π解析 根据几何体的三视图可知,该几何体是一个正方体和一个半圆柱的组合体,其中正方体的棱长为 2,半圆柱的底面半径为 1,母线...