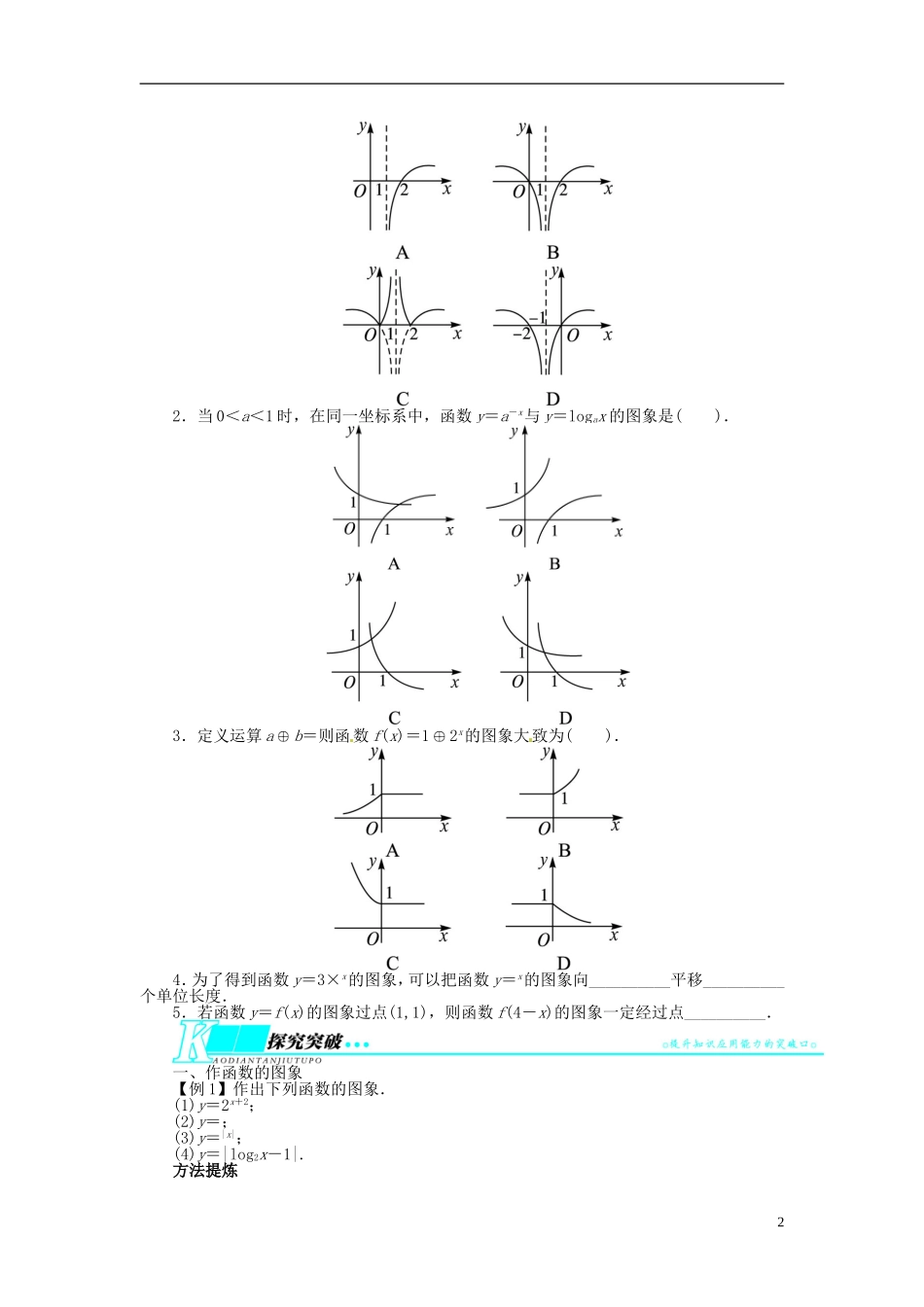
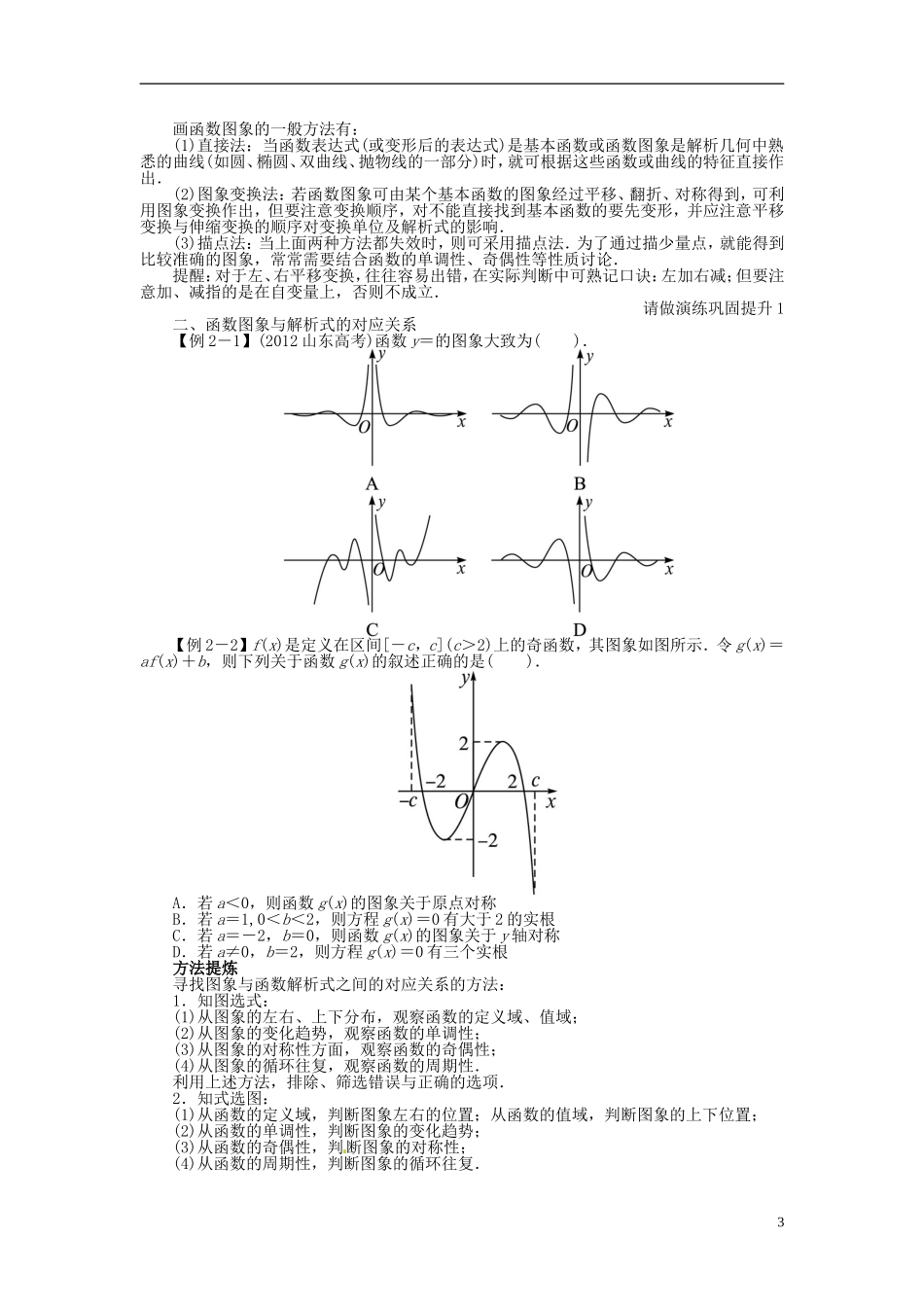
2.8 函数的图象及其变换考纲要求1.掌握基本初等函数的图象的特征,能熟练运用基本初等函数的图象解决问题.2.掌握图象的作法:描点法和图象变换法.3.会运用函数图象理解和研究函数的性质.1.作图:作函数图象有两种基本方法(1)描点法其基本步骤是列表、描点、连线.首先:① 确定函数的______;② 化简函数______;③ 讨论函数的性质(_____、_____、_____、_____等);其次:列表(尤其注意特殊点、零点、最高点、最低点、与坐标轴的交点);再次:描点;最后:连线.(2)图象变换法① 平移变换左右平移:y=f(x±a)(a>0)的图象,可由 y=f(x)的图象向____(+)或向____(-)平移____个单位而得到.上下平移:y=f(x)±b(b>0)的图象,可由 y=f(x)的图象向____(+)或向____(-)平移____个单位而得到.② 对称变换y=f(-x)与 y=f(x)的图象关于____对称.y=-f(x)与 y=f(x)的图象关于____对称.y=-f(-x)与 y=f(x)的图象关于____对称.要得到 y=|f(x)|的图象,可将 y=f(x)的图象在 x 轴下方的部分以 x 轴为对称轴翻折到 x 轴上方,其余部分不变而得到.要得到 y=f(|x|)的图象,可将 y=f(x),x≥0 的部分作出,再利用偶函数的图象关于____的对称性,作出 x<0 的图象而得到.③ 伸缩变换y=Af(x)(A>0)的图象,可将 y=f(x)图象上所有点的纵坐标变为原来的____倍,横坐标不变而得到.y=f(ax)(a>0)的图象,可将 y=f(x)图象上所有点的横坐标变为________,纵坐标不变而得到.2.有关函数图象的几个结论(1)若 f(a+x)=f(b-x),x∈R 恒成立,则 y=f(x)的图象关于______成轴对称图形;(2)函数 y=f(a+x)与函数 y=f(b-x)的图象关于直线______对称.(3)若定义在 R 上的函数 f(x)关于直线 x=a 与 x=b(b>a)都对称,则 f(x)为周期函数,______是它的一个周期(未必是最小正周期,下同).(4)若定义在 R 上的函数关于点(a,c)和(b,c)(b>a)都成中心对称,则 f(x)为周期函数,______是它的一个周期.(5)若定义在 R 上的函数 f(x)的图象关于点(a,c)成中心对称,又关于直线 x=b(b>a)成轴对称,则 f(x)是周期函数,______是它的一个周期.1.函数 y=lg |x-1|的图象大致为( ).12.当 0<a<1 时,在同一坐标系中,函数 y=a-x与 y=logax 的图象是( ).3.定义运算 ab=则函数 f(x)=12x的图象大致为( ).4.为了得到函数 y=3×x的图象,可以把函数 y=x的图象向_______...