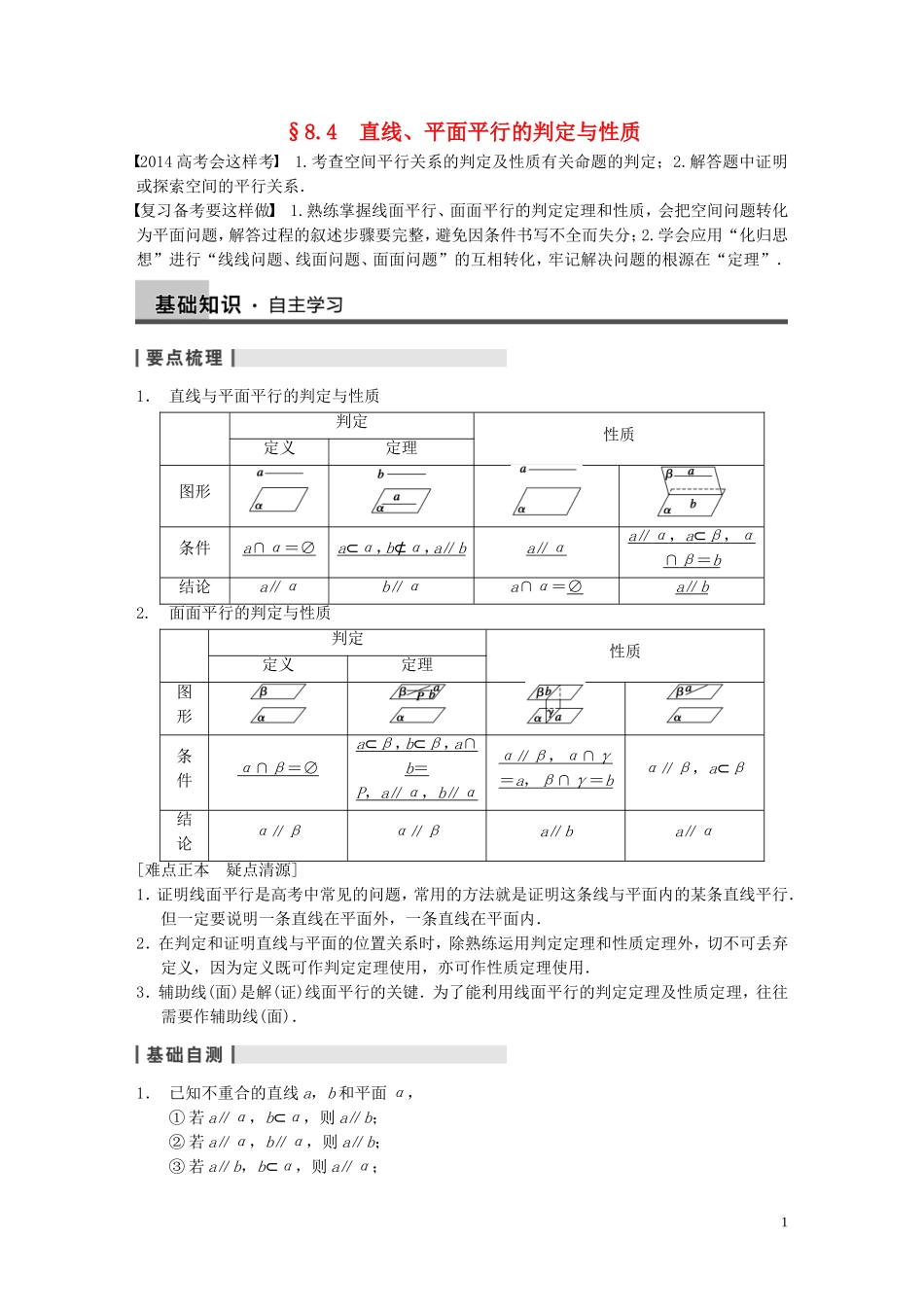
§8.4 直线、平面平行的判定与性质2014 高考会这样考 1.考查空间平行关系的判定及性质有关命题的判定;2.解答题中证明或探索空间的平行关系.复习备考要这样做 1.熟练掌握线面平行、面面平行的判定定理和性质,会把空间问题转化为平面问题,解答过程的叙述步骤要完整,避免因条件书写不全而失分;2.学会应用“化归思想”进行“线线问题、线面问题、面面问题”的互相转化,牢记解决问题的根源在“定理”.1. 直线与平面平行的判定与性质判定性质定义定理图形条件a ∩ α = ∅ a ⊂ α , b ⊄ α , a ∥ b a ∥ α a ∥ α , a ⊂ β , α ∩ β = b 结论a∥αb∥αa∩α=∅a ∥ b 2. 面面平行的判定与性质判定性质定义定理图形条件α ∩ β = ∅ a ⊂ β , b ⊂ β , a ∩ b = P , a ∥ α , b ∥ α α ∥ β , α ∩ γ = a , β ∩ γ = b α∥β,a⊂β结论α∥βα∥βa∥ba∥α[难点正本 疑点清源]1.证明线面平行是高考中常见的问题,常用的方法就是证明这条线与平面内的某条直线平行.但一定要说明一条直线在平面外,一条直线在平面内.2.在判定和证明直线与平面的位置关系时,除熟练运用判定定理和性质定理外,切不可丢弃定义,因为定义既可作判定定理使用,亦可作性质定理使用.3.辅助线(面)是解(证)线面平行的关键.为了能利用线面平行的判定定理及性质定理,往往需要作辅助线(面).1. 已知不重合的直线 a,b 和平面 α,① 若 a∥α,b⊂α,则 a∥b;② 若 a∥α,b∥α,则 a∥b;③ 若 a∥b,b⊂α,则 a∥α;1④ 若 a∥b,a∥α,则 b∥α 或 b⊂α.上面命题中正确的是________(填序号).答案 ④解析 ①若 a∥α,b⊂α,则 a,b 平行或异面;②若 a∥α,b∥α,则 a,b 平行、相交、异面都有可能;③若 a∥b,b⊂α,则 a∥α 或 a⊂α.2. 已知 α、β 是不同的两个平面,直线 a⊂α,直线 b⊂β,命题 p:a 与 b 没有公共点;命题q:α∥β,则 p 是 q 的____________条件.答案 必要不充分解析 a 与 b 没有公共点,不能推出 α∥β,而 α∥β 时,a 与 b 一定没有公共点,即 pD⇒/q,q⇒p,∴p 是 q 的必要不充分条件.3. 已知平面 α∥平面 β,直线 a⊂α,有下列命题:①a 与 β 内的所有直线平行;② a 与 β 内无数条直线平行;③...