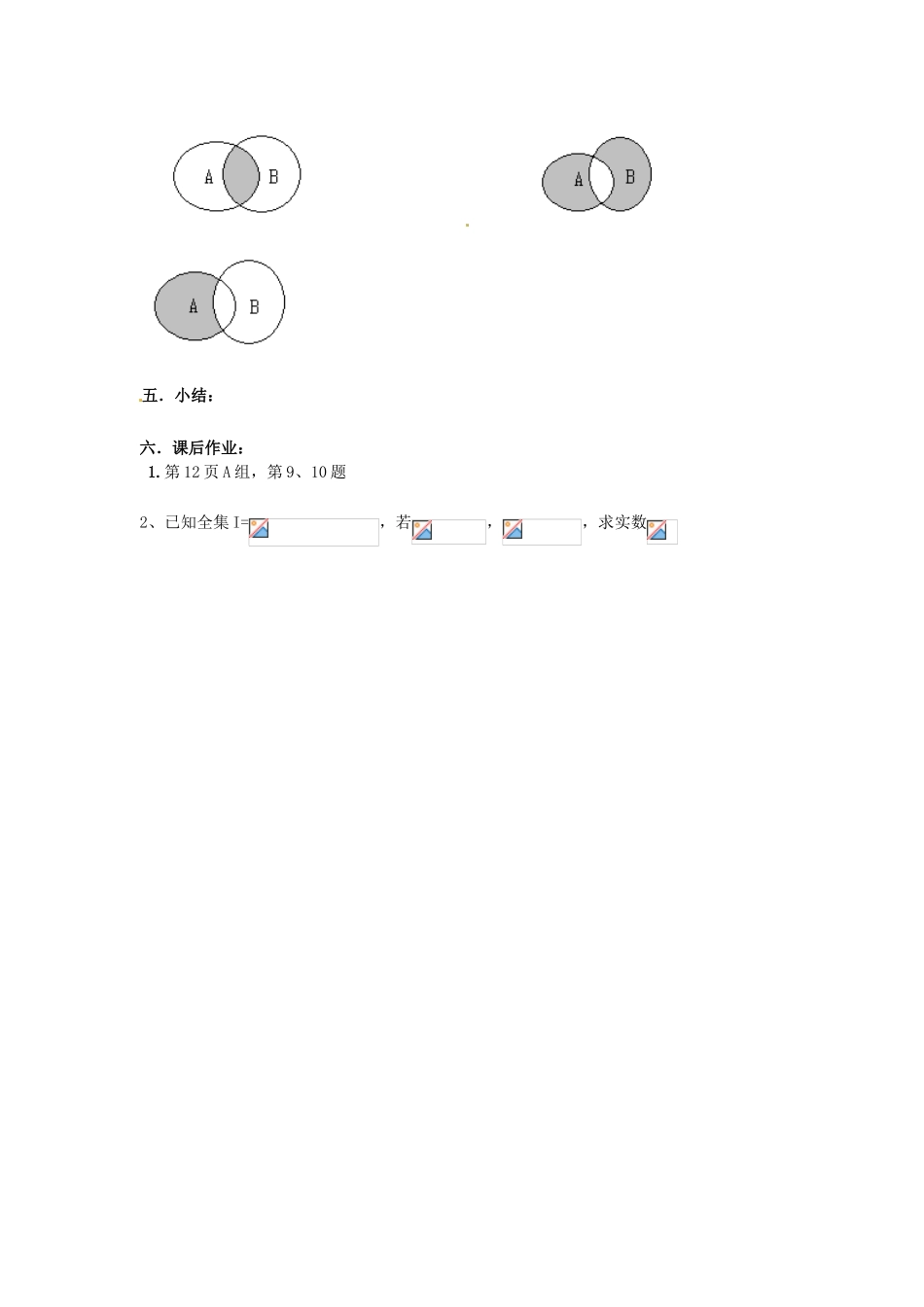
1.1.3 集合的基本运算(二)(学案)一.学习要点:并集与交集的基本性质及补集的概念和性质二.复习:并集和交集的概念三.新课学习:一.并集和交集的性质:1.A∩B ,A∩B ,A∩A= ,A∩= ,A∩B=B∩A2. A∪B, A∪B,A∪A= ,A∪= ,A∪B=B∪A3.若 A∩B=A,则 ,反之也成立,即:4.若 A∪B=B, 则 ,反之也成立,即:5.若x∈(A∩B),则 6.若 x∈(A∪B),则 二.全集:在给定的问题中,若研究的所有 集合都是某一给定集合 的 ,那么称这个给定 的集合为 .三.若 A 是全集 U 的子集,由 U 中 A 的元素构成的集合,叫做 A 在 U 中的 ,记作 四.补集的基本性质 , , , 例 1 设 U={x|x 是小于 9 的正整数},A={1,2,3} B={3,4,5,6},求UA、UB,(UA)∩(UB),(UA)∪(UB).例 2 设全集 U={x|x 是三角形 },A={x|x 是锐角三角形}, B={x|x 是钝角 三角形},求 A∩B, U(A∪B).四.课堂练习:1. 第 11 页练习第 4 题2.分别用集合 A,B 表示下图的阴影部分 五.小结: 六.课后作业: 1.第 12 页 A 组,第 9、10 题 2、已知全集 I=,若,,求实数