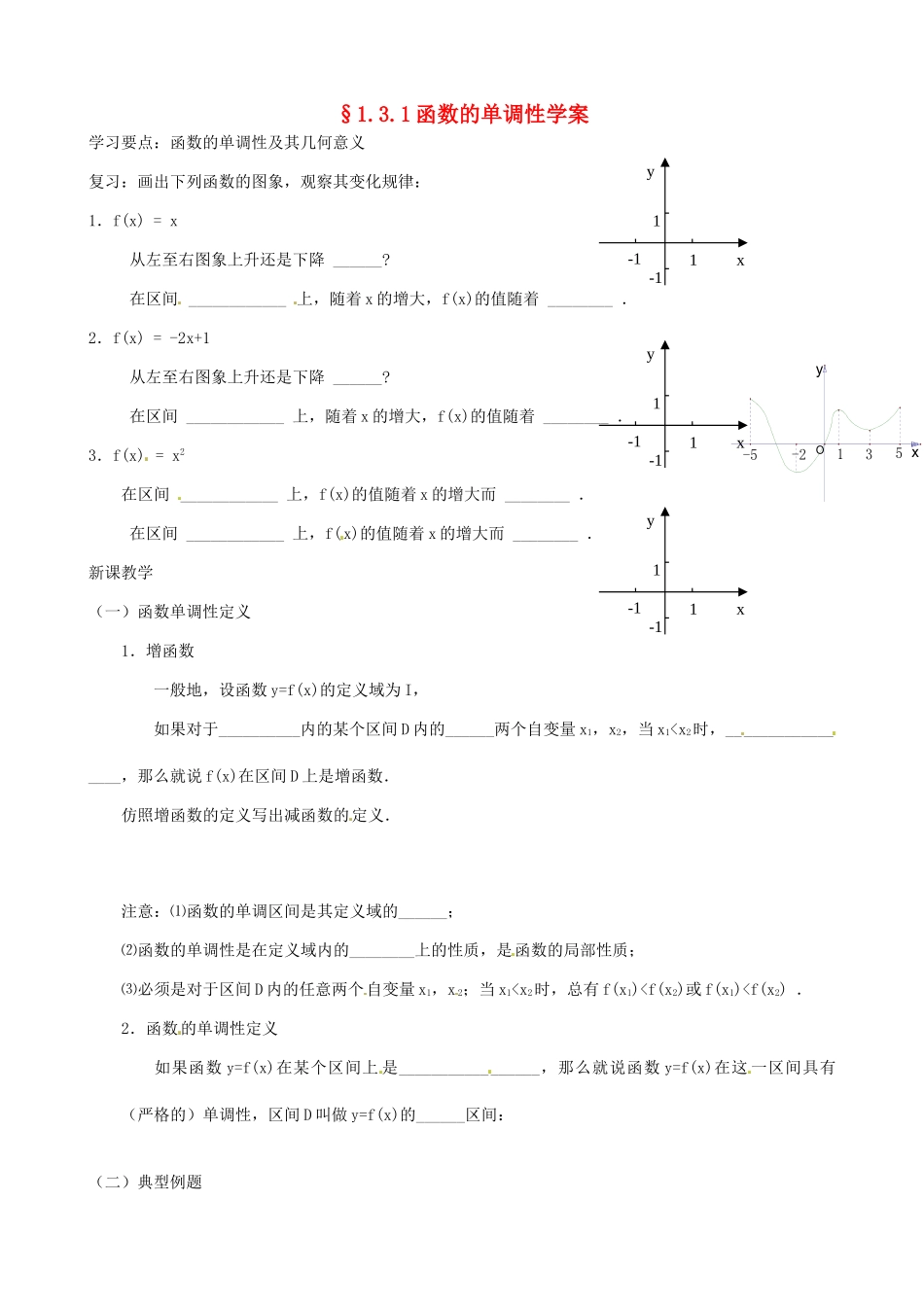
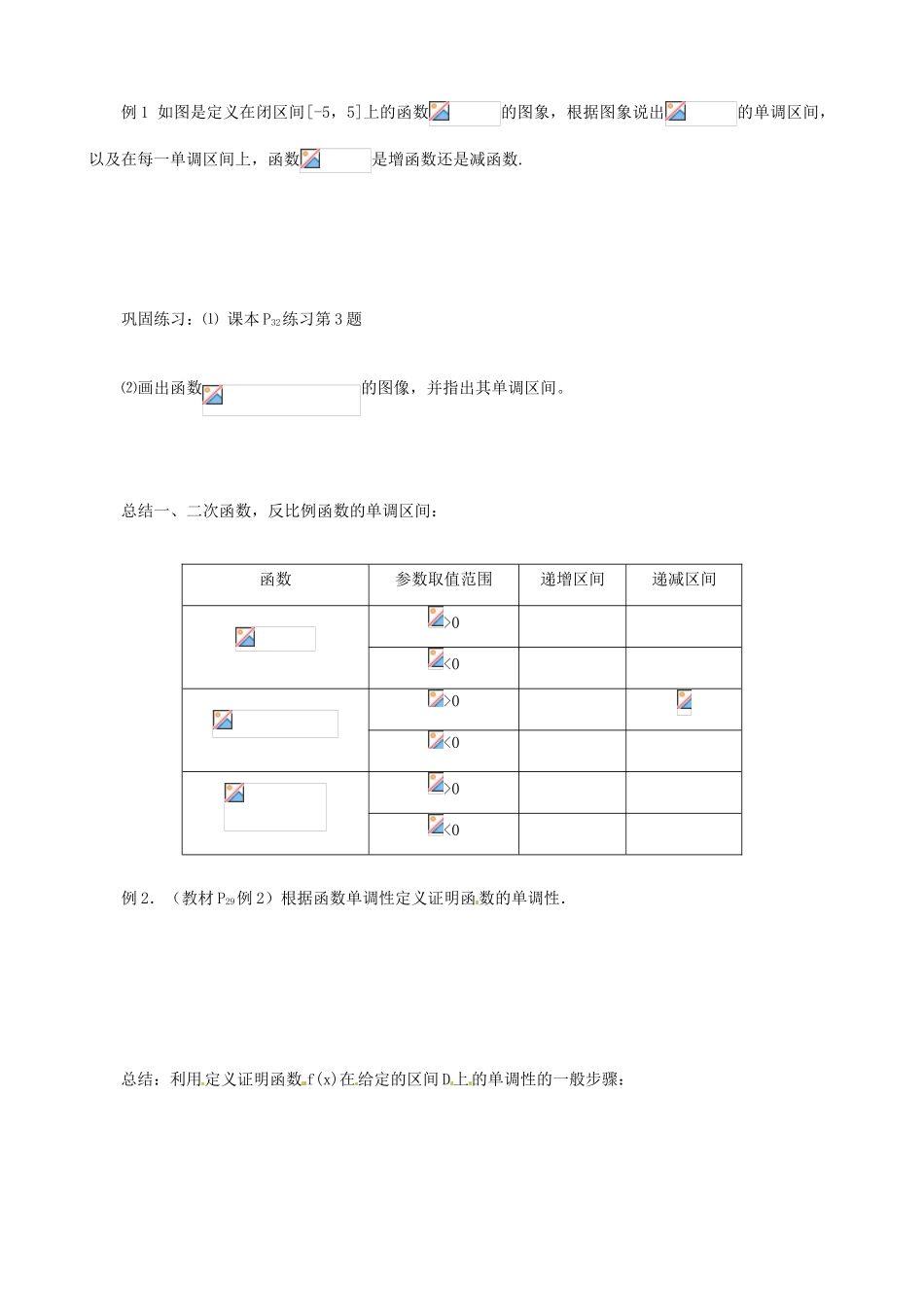
§1.3.1 函数的单调性学案学习要点:函数的单调性及其几何意义复习:画出下列函数的图象,观察其变化规律:1.f(x) = x 从左至右图象上升还是下降 ______? 在区间 ____________ 上,随着 x 的增大,f(x)的值随着 ________ .2.f(x) = -2x+1 从左至右图象上升还是下降 ______? 在区间 ____________ 上,随着 x 的增大,f(x)的值随着 ________ .3.f(x) = x2在区间 ____________ 上,f(x)的值随着 x 的增大而 ________ . 在区间 ____________ 上,f(x)的值随着 x 的增大而 ________ .新课教学(一)函数单调性定义1.增函数一般地,设函数 y=f(x)的定义域为 I,如果对于__________内的某个区间 D 内的______两个自变量 x1,x2,当 x10 <0 >0<0>0<0例 2.(教材 P29例 2)根据函数单调性定义证明函数的单调性.总结:利用定义证明函数 f(x)在给定的区间 D上的单调性的一般步骤: ⑤ 巩固练习:⑴ 课本P32练习第 4 题⑵证明函数在(1,+∞)上为增函数.⑶画出反比例函数的图象. 这个函数的定义域是什么? 它在定义域 I 上的单调性怎样?证明你的结论.课后作业1.课本 P39 习题 1.3(A 组) 第 1、2 题.2. 函数 y==x2-6x+10 在区间(2,4)上是( ) A.递减函数B.递增函数 C.先递减再递增D.选递增再递减.3. 附加题:⑴函数 f(x)=-+2(a-1)x+2 在(-∞,4)上是增函数,则 a 的范围是( ) A.a≥5B.a≥3C.a≤3D.a≤-5⑵讨论函数在(-2,2)内的单调性.