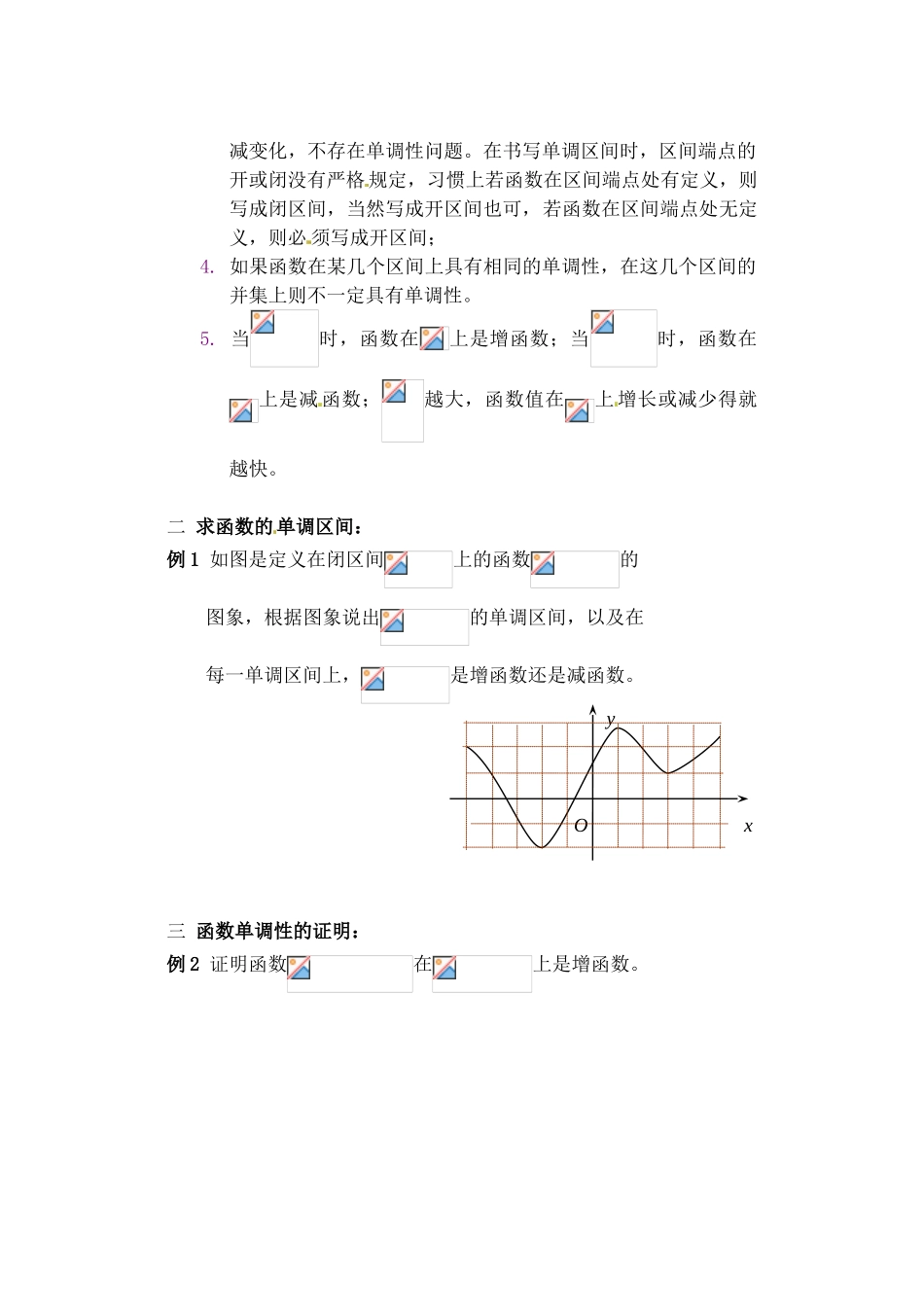
2.1.3 函数的单调性一.学习要点:函数的单调性的概念及其简单应用二.学习过程:引例:考察函数,,的图象。问题:当自变量在实数集内由小变大时,函数的值怎样变化?一 函数单调性的定义:在函数的图象上任取两点、,记,.——自变量的改变量,——因变量的改变量。一般地,设函数的定义域为,区间.1. 增函数:对任意两个值,当改变量时,有,那么 就称函数在区间上是增函数;2. 减函数:对任意两个值,当改变量时,有,那么就称函数在区间上是减函数。3. 单调 性:如果一个函数在某个区间上是增函数或是减函数,就说这个函数在这个区间上具有单调性(区间称为单调区间)。注意:1. 定义 中的,应满足三个条件:同属于一个单调区间;具有任意性;规定大小;2. 函数的单调性是对某个区间而言的,函数的单调区间为函数定义域的子区间;3. 对于单独的一个点由于它的函数值是唯一的常数,因而没有增减变化,不存在单调性问题。在书写单调区间时,区间端点的开或闭没有严格 规定,习惯上若函数在区间端点处有定义,则写成闭区间,当然写成开区间也可,若函数在区间端点处无定义,则必 须写成开区间;4. 如果函数在某几个区间上具有相同的单调性,在这几个区间的并集上则不一定具有单调性。5. 当时,函数在上是增函数;当时,函数在上是减 函数;越大,函数值在上 增长或减少得就越快。二 求函数的单调区间:例 1 如图是定义在闭区间上的函数的图象,根据图象说出的单调区间,以及在每一单调区间上,是增函数还是减函数。三 函数单调性的证明:例 2 证明函数在上是增函数。xyO例 3 证明函数在区间和上分别是减函数。四 函数单调性的应用:例 4 已知函数在区间上是减函数,求实数的取值范围。课堂练习:1.设函数是上的减函数,则有( ) A . B . C . D.2.函数的单调递减区间是( ) A. B. C. D.3.下列函数中,在区间上为增函数的是( ) A. B. C. D.4.函数在上为增函数,则实数的取值范围是________________5.函数的单调减区间是________________6.函数的单调减区间是________________7.函数的图象如图,则函数的单调减区间是________________8.函数在上递增,则的范围为______________9.求证在为增函数。xyO10 . 对 于 给 定 区 间 上 任 意 两 个 值,,,,① 当时,函数在区间上为增函数② 当时,函数在区间上为减函数③ 当时,函数在区间上的单调性不确定...