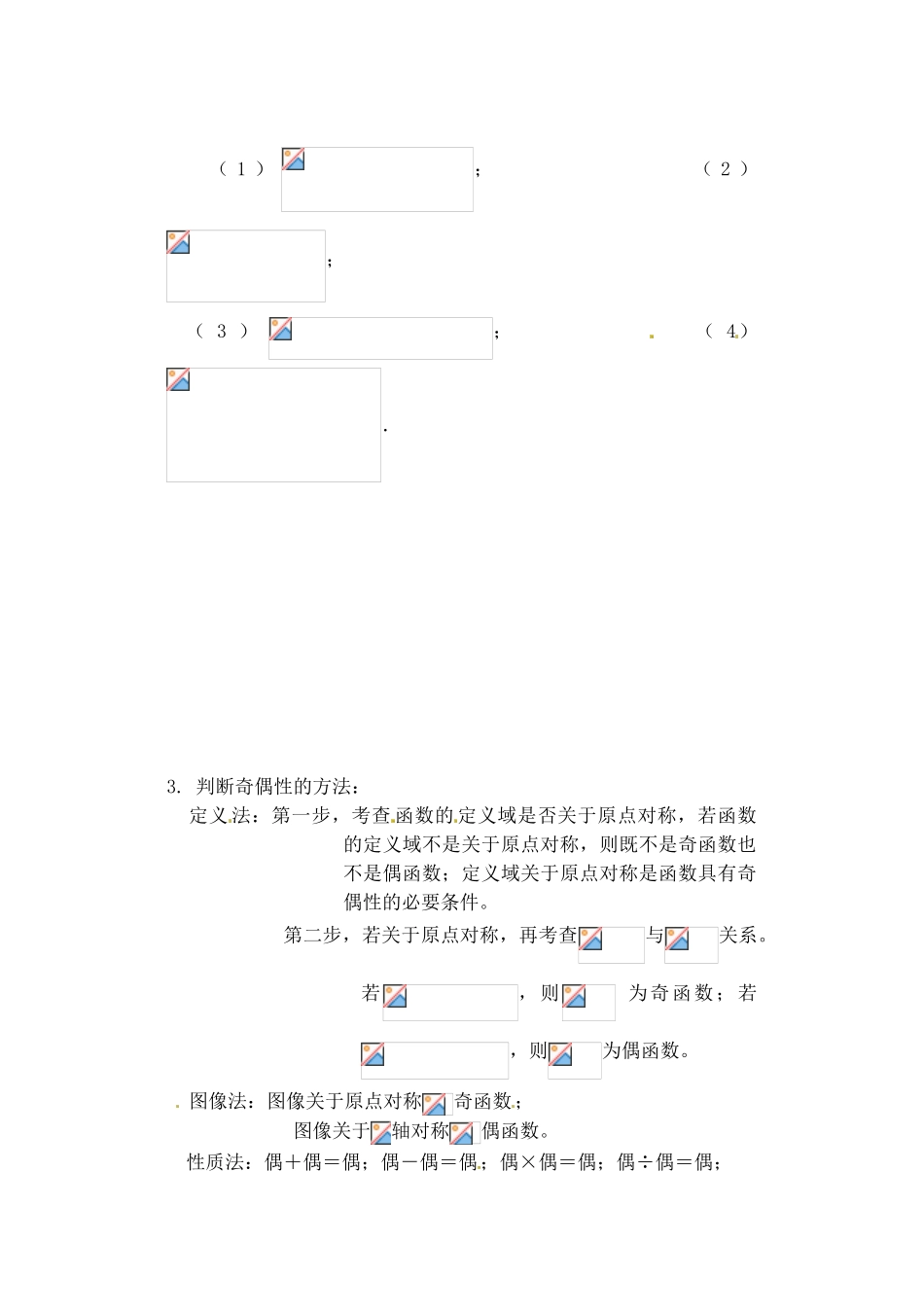
2.1.4 函数的奇偶性一.学习要点:函数的奇偶性的定义、性质及其简单应用二.学习过程:引例:已知函数,,则有 , 讨论与、与的关系。1. 函数奇偶性的定义:奇函数:设函数的定义 域为,如果对内的任意一个,都有,且,则 这个函数叫做奇函数。偶函数:设函数的定义域为,如果 对内的任意一个,都有,且,则这个函数叫做偶函数。非奇非偶函数:既不是奇函数也不是偶函数的函数叫做非奇非偶函数。奇偶性:如果一个函数在其定义域上是奇函数或是偶函数,则称函数具有奇偶性。注意:(1) “对任意,都有”,说明函数的定义域关于原点对称,这是函数具有 奇偶性的必要条件。否则,如果一个函数的定义域不关于原点对称,那么它就不具有奇偶性;(2)如果一个函数的定义域关于原点对称,那么这个函数也未必具 有 奇 偶 性 , 还 需 判 断是 否 等 于, 或 判 断是否等于零,或判断是否等于等等。(3) 从函数奇偶性的角度,可将函数分为奇函 数、偶函数、非奇非偶函数以及既是奇函数又是偶函数;2 函数奇偶性的性质:(1)如果一个函数是奇函数,则这个函数的图 像是以坐标原点为对称中心的中心对称图形;反之,如果一个函数的图像是以坐标原点为对称的中心对称图形,则这个函数是奇函数。(2)如果一个函数是偶函数,则它的图像是以轴为对称轴的轴对称图形;反之,如果一个函数的图像关于轴对称,则这个函数是偶函数。注意:(1) 若奇函数在处有定义,则;( 2 ) 既 是 奇 函 数 又 是 偶 函 数 的 函 数 图 象 在轴 上 。 如是既奇又偶函数;(3) 从区间看:函数的奇偶性是“整体”性质,单调性是“局部”性质。从图像看:函数的奇偶性体现的是对称性,单调性体现的是升降性。例 1 判断下列函数是否具有奇偶性:(1); (2);(3); (4).例 2 判断下列函数是否具有奇偶性: ( 1 ); ( 2 ); ( 3 ); ( 4).3. 判断奇偶性的方法: 定义 法:第一步,考查 函数的 定义域是否关于原点对称,若函数的定义域不是关于原点对称,则既不是奇函数也不是偶函数;定义域关于原点对称是函数具有奇偶性的必要条件。第二步,若关于原点对称,再考查与关系。若,则 为奇函数;若,则为偶函数。 图像法:图像关于原点对称奇函数; 图像关于轴对称偶函数。 性质法:偶+偶=偶;偶-偶=偶;偶×偶=偶;偶÷偶=偶;奇+奇=奇;奇-奇=奇;奇×奇=偶...