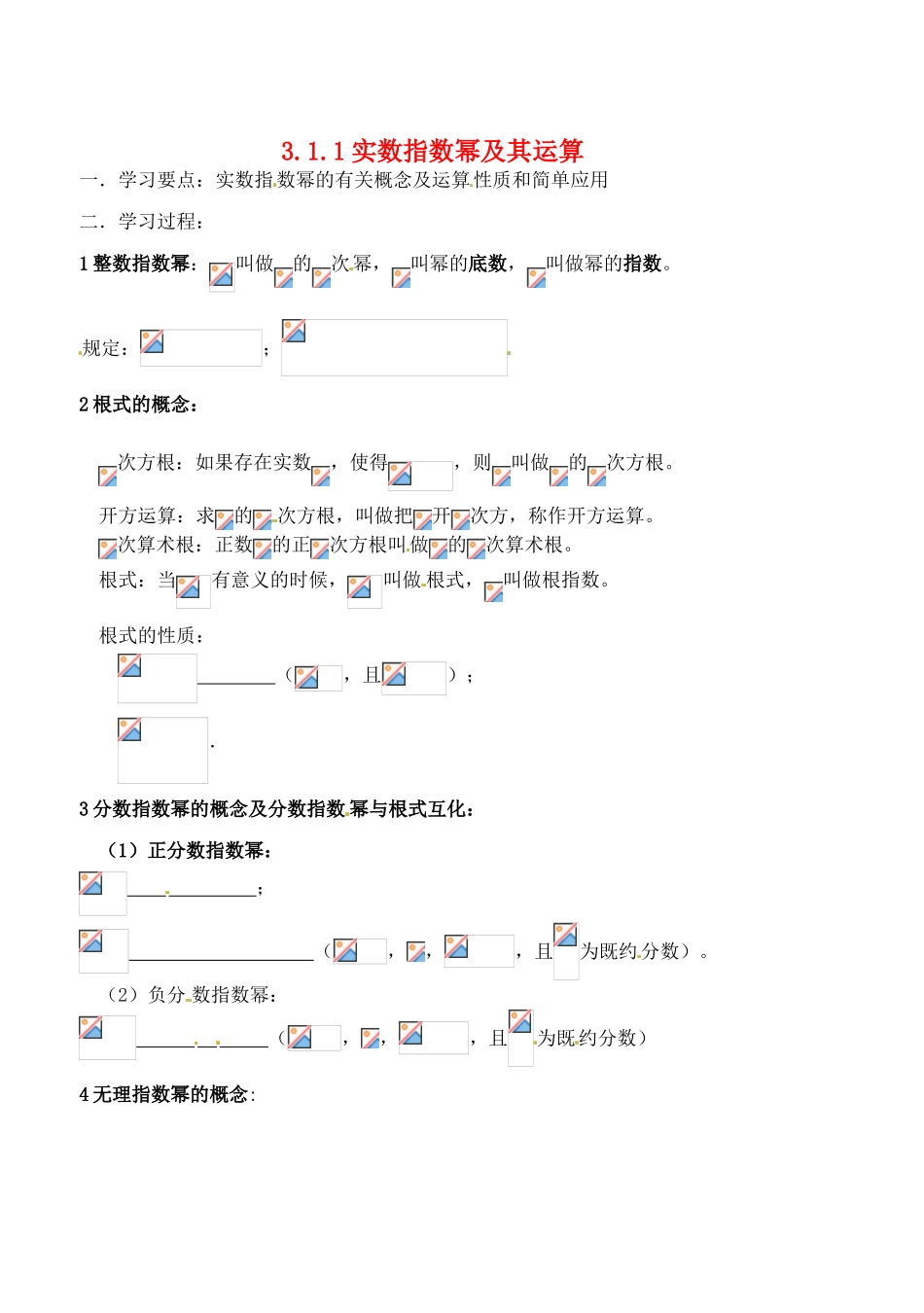
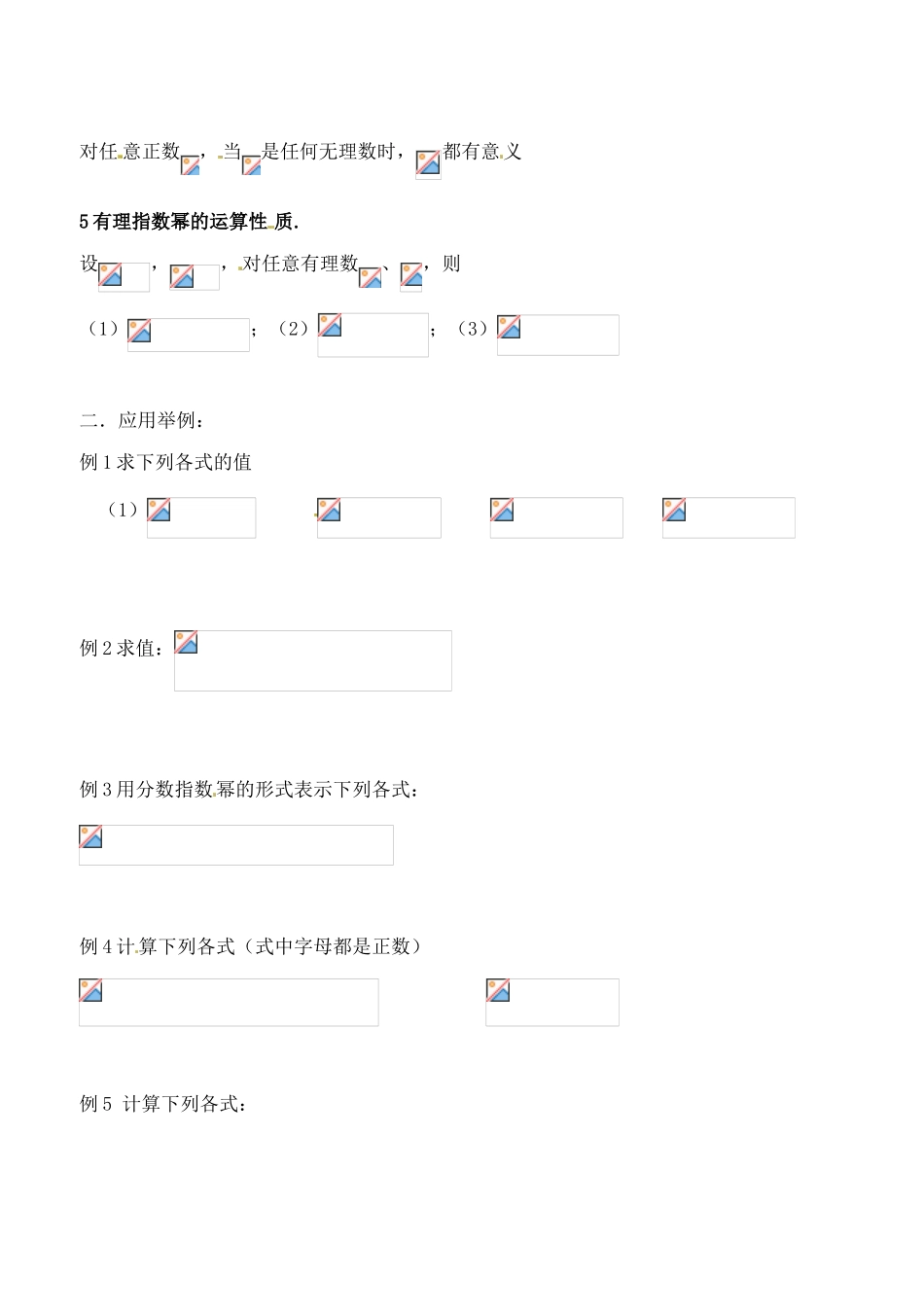
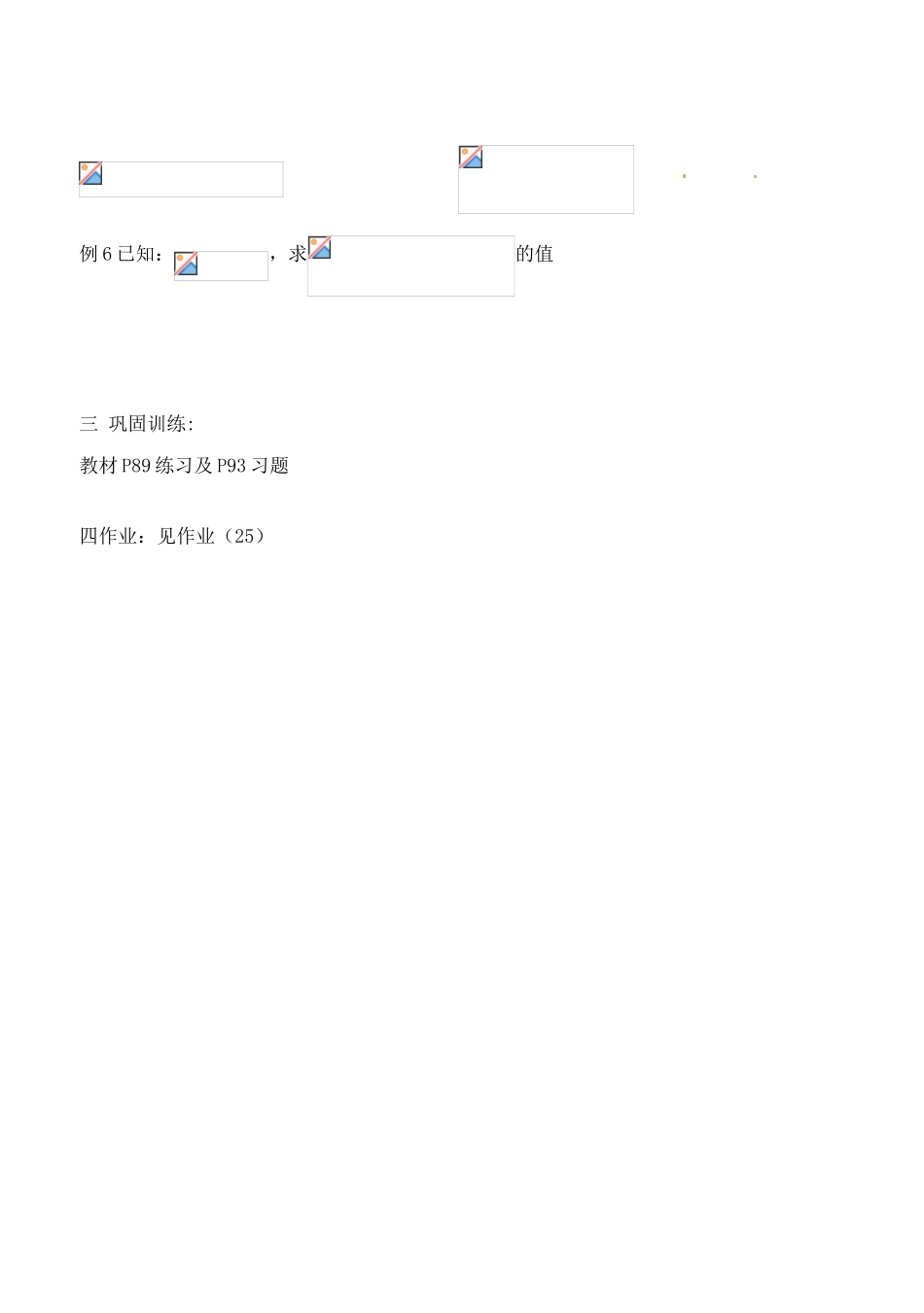
3.1.1 实数指数幂及其运算一.学习要点:实数指数幂的有关概念及运算性质和简单应用二.学习过程:1 整数指数幂:叫做的次幂,叫幂的底数,叫做幂的指数。规定:;2 根式的概念:次方根:如果存在实数,使得,则叫做的次方根。开方运算:求的次方根,叫做把开次方,称作开方运算。次算术根:正数的正次方根叫做的次算术根。根式:当有意义的时候,叫做 根式,叫做根指数。根式的性质: (,且);.3 分数指数幂的概念及分数指数 幂与根式互化:(1)正分数指数幂: ; (,,,且为既约分数)。(2)负分 数指数幂: (,,,且为既约分数)4 无理指数幂的概念:对任 意正数, 当是任何无理数时,都有意义5 有理指数幂的运算性 质.设,,对任意有理数、,则(1);(2);(3)二.应用举例:例 1 求下列各式的值(1) 例 2 求值:例 3 用分数指数幂的形式表示下列各式:例 4 计算下列各式(式中字母都是正数) 例 5 计算下列各式: 例 6 已知:,求的值三 巩固训练:教材 P89 练习及 P93 习题四作业:见作业(25)