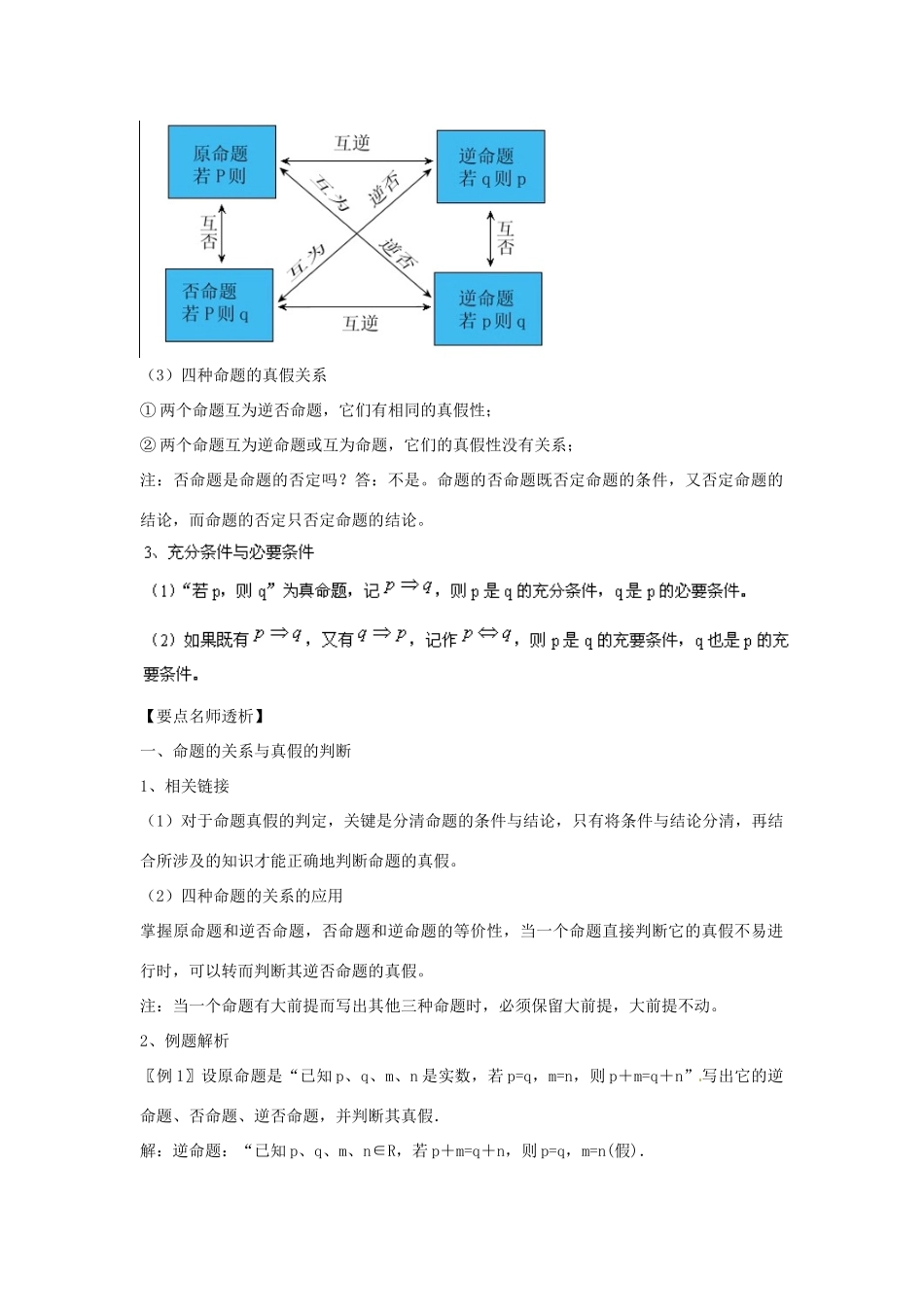
四川省古蔺县中学高三数学复习学案:1.2 命题及其关系、充分条件与必要条件【高考目标导航】一、考纲点击1、理解命题的概念;2、了解“若 p,则 q”形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系;3、理解必要条件、充分条件与充要条件的意义。二、热点、难点提示1、充分必要条件的判断和四种命题及其关系是本节考查的热点;2、多以选择题、填空题的形式出现,由于知识载体丰富,具有较强的综合性,属于中、低档题目;有时也在解答题中出现,考查对概念的理解与应用,难度不会太大。【考纲知识梳理】1、命题用语言、符号或式子表达的,可以判断真假的陈述句叫做命题,其中判断为真的语句叫做真命题,判断为假的语句叫做假命题。2、四种命题及其关系(1)四种命题(2)四种命题间的相互关系(3)四种命题的真假关系① 两个命题互为逆否命题,它们有相同的真假性;② 两个命题互为逆命题或互为命题,它们的真假性没有关系;注:否命题是命题的否定吗?答:不是。命题的否命题既否定命题的条件,又否定命题的结论,而命题的否定只否定命题的结论。【要点名师透析】一、命题的关系与真假的判断1、相关链接(1)对于命题真假的判定,关键是分清命题的条件与结论,只有将条件与结论分清,再结合所涉及的知识才能正确地判断命题的真假。(2)四种命题的关系的应用掌握原命题和逆否命题,否命题和逆命题的等价性,当一个命题直接判断它的真假不易进行时,可以转而判断其逆否命题的真假。注:当一个命题有大前提而写出其他三种命题时,必须保留大前提,大前提不动。2、例题解析〖例 1〗设原命题是“已知 p、q、m、n 是实数,若 p=q,m=n,则 p+m=q+n”写出它的逆命题、否命题、逆否命题,并判断其真假.解:逆命题:“已知 p、q、m、n∈R,若 p+m=q+n,则 p=q,m=n(假).原命题:“已知 p、q、m、n∈R,若 p≠q,m≠n,则 p+m≠q+n”(假)逆否命题:“已知 p、q、m、n∈R,若 p+m≠q+n,则 p≠q 或 m≠n”(真)注,否命题“若 p≠q,m≠n”应理解为“p≠q 或 m≠n”即是指:① p≠q,但 m=n,② p=q 但 m≠n,而不含 p≠q 且 m≠n.因为原命题中的条件:“若 p=q,m=n.”应理解为“若 p=q 且 m=n,”而这一语句的否定应该是“p≠q 或m≠n”.〖例 2〗以下列命题为原命题,分别写出它们的逆命题,否命题和逆否命题.① 内接于圆的四边形的对角互补;② 已知 a、b、c、d 是实数,若 a...