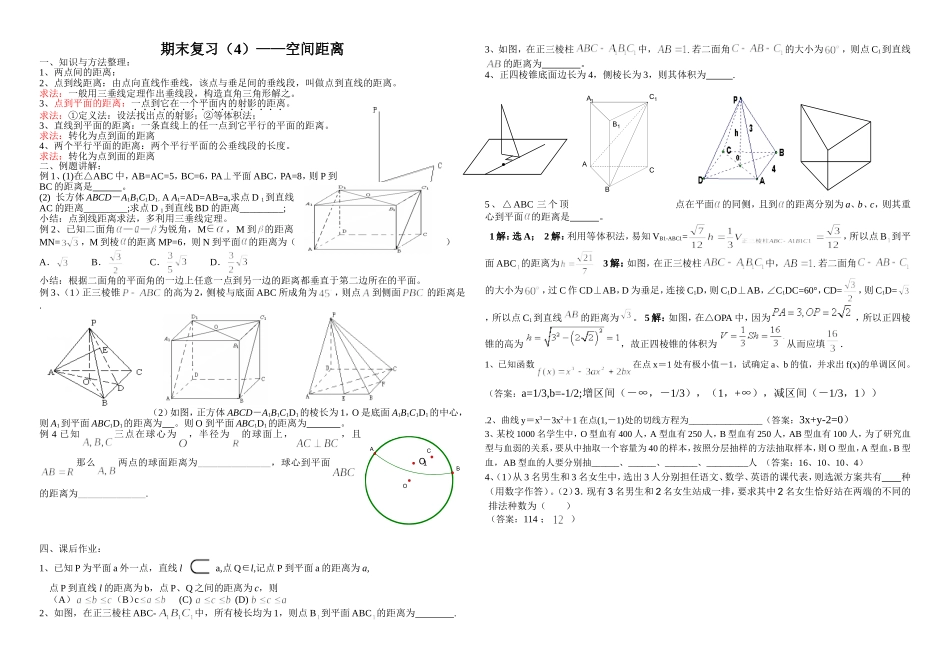
期末复习(4)——空间距离一、知识与方法整理:1、两点间的距离:2、点到线距离:由点向直线作垂线,该点与垂足间的垂线段,叫做点到直线的距离。求法:一般用三垂线定理作出垂线段,构造直角三角形解之。3、点到平面的距离:一点到它在一个平面内的射影的距离。求法:①定义法:设法找出点的射影;②等体积法;3、直线到平面的距离:一条直线上的任一点到它平行的平面的距离。求法:转化为点到面的距离4、两个平行平面的距离:两个平行平面的公垂线段的长度。求法:转化为点到面的距离二、例题讲解:例 1、(1)在△ABC 中,AB=AC=5,BC=6,PA⊥平面 ABC,PA=8,则 P 到BC 的距离是 。(2) 长方体 ABCD-A1B1C1D1,A A1=AD=AB=a,求点 D 1到直线AC 的距离_________;求点 D 1到直线 BD 的距离_________;小结:点到线距离求法,多利用三垂线定理。例 2、已知二面角— —为锐角,M,M 到的距离MN=,M 到棱的距离 MP=6,则 N 到平面的距离为( )A. B. C. D.小结:根据二面角的平面角的一边上任意一点到另一边的距离都垂直于第二边所在的平面。例 3、(1)正三棱锥的高为 2,侧棱与底面 ABC 所成角为,则点到侧面的距离是 .(2)如图,正方体 ABCD-A1B1C1D1的棱长为 1,O 是底面 A1B1C1D1的中心,则 A1到平面 ABC1D1的距离为 。则 O 到平面 ABC1D1的距离为 。例 4 已知三点在球心为,半径为的球面上,,且那么两点的球面距离为_______________,球心到平面的距离为______________.四、课后作业:1、已知 P 为平面 a 外一点,直线 la,点 Q∈l,记点 P 到平面 a 的距离为 a,点 P 到直线 l 的距离为 b,点 P、Q 之间的距离为 c,则(A)(B)c (C) (D) 2、如图,在正三棱柱 ABC-中,所有棱长均为 1,则点 B 到平面 ABC 的距离为 .3、如图,在正三棱柱中,若二面角的大小为,则点 C1到直线的距离为 。4、正四棱锥底面边长为 4,侧棱长为 3,则其体积为 . 5 、 △ ABC 三 个 顶点在平面的同侧,且到的距离分别为 a、b、c,则其重心到平面的距离是 。1 解:选 A; 2 解:利用等体积法,易知 VB1-ABC1=,所以点 B 到平面 ABC 的距离为 3 解:如图,在正三棱柱中,若二面角的大小为,过 C 作 CD⊥AB,D 为垂足,连接 C1D,则 C1D⊥AB,∠C1DC=60°,CD=,则 C1D=,所以点 C1到直线的距离为。 5 解:如图,在△OPA 中,因为 ,所以正四棱锥...