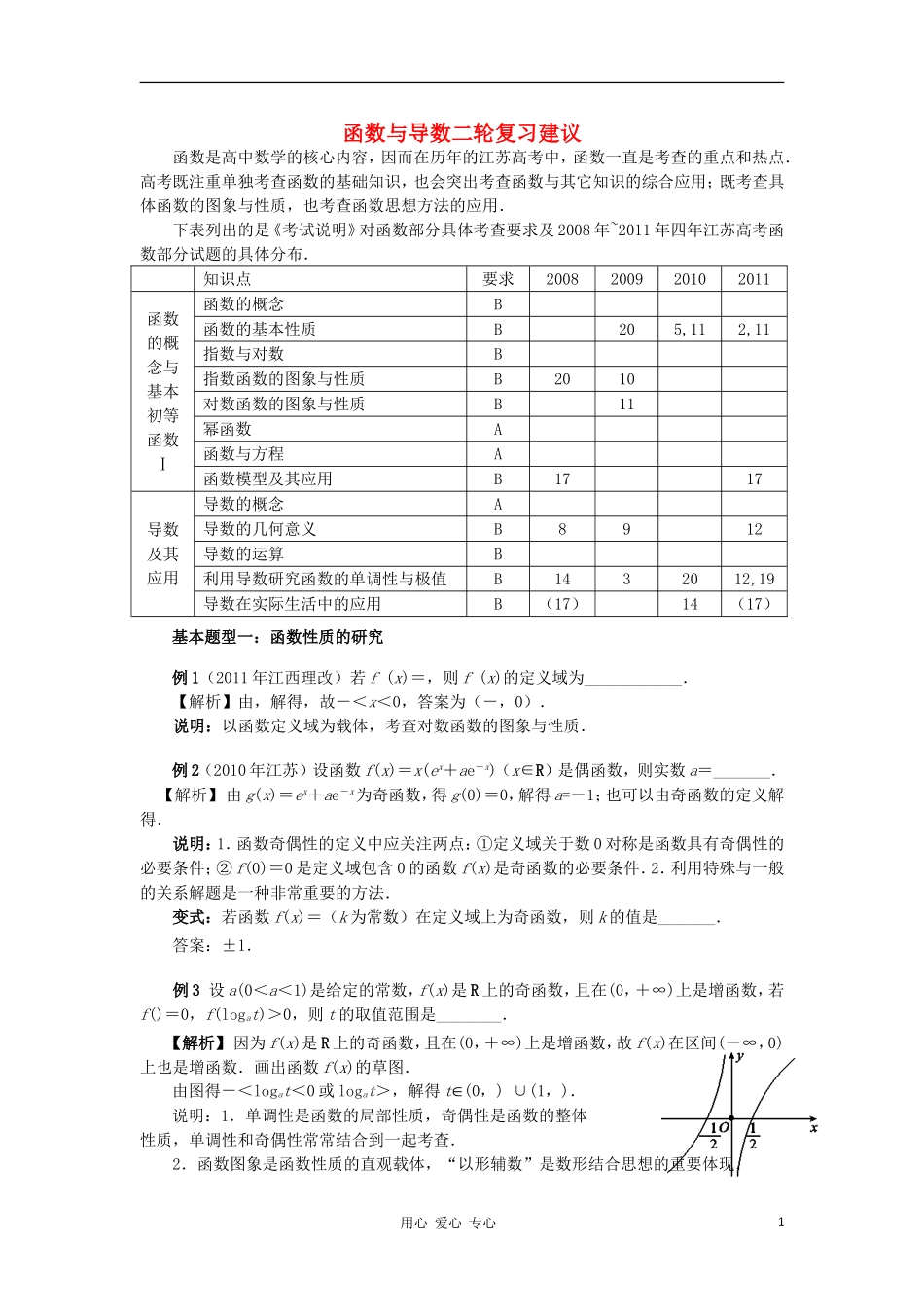
函数与导数二轮复习建议函数是高中数学的核心内容,因而在历年的江苏高考中,函数一直是考查的重点和热点.高考既注重单独考查函数的基础知识,也会突出考查函数与其它知识的综合应用;既考查具体函数的图象与性质,也考查函数思想方法的应用. 下表列出的是《考试说明》对函数部分具体考查要求及 2008 年~2011 年四年江苏高考函数部分试题的具体分布.知识点要求2008200920102011函数的概念与基本初等函数Ⅰ函数的概念B函数的基本性质B205,112,11指数与对数B指数函数的图象与性质B2010对数函数的图象与性质B11幂函数A函数与方程A函数模型及其应用B1717导数及其应用导数的概念A导数的几何意义B8912导数的运算B利用导数研究函数的单调性与极值B1432012,19导数在实际生活中的应用B(17)14(17)基本题型一:函数性质的研究例 1(2011 年江西理改)若 f (x)=,则 f (x)的定义域为____________.【解析】由,解得,故-<x<0,答案为(-,0).说明:以函数定义域为载体,考查对数函数的图象与性质.例 2(2010 年江苏)设函数 f(x)=x(ex+ae-x)(x∈R)是偶函数,则实数 a=_______.【解析】 由 g(x)=ex+ae-x为奇函数,得 g(0)=0,解得 a=-1;也可以由奇函数的定义解得.说明:1.函数奇偶性的定义中应关注两点:①定义域关于数 0 对称是函数具有奇偶性的必要条件;② f(0)=0 是定义域包含 0 的函数 f(x)是奇函数的必要条件.2.利用特殊与一般的关系解题是一种非常重要的方法.变式:若函数 f(x)=(k 为常数)在定义域上为奇函数,则 k 的值是_______.答案:±1.例 3 设 a(0<a<1)是给定的常数,f(x)是 R 上的奇函数,且在(0,+∞)上是增函数,若f()=0,f(logat)>0,则 t 的取值范围是________.【解析】 因为 f(x)是 R 上的奇函数,且在(0,+∞)上是增函数,故 f(x)在区间(-∞,0)上也是增函数.画出函数 f(x)的草图.由图得-<logat<0 或 logat>,解得 t(0,) ∪(1,).说明:1.单调性是函数的局部性质,奇偶性是函数的整体性质,单调性和奇偶性常常结合到一起考查. 2.函数图象是函数性质的直观载体,“以形辅数”是数形结合思想的重要体现.用心 爱心 专心1例 4(2010 年江苏卷)已知函数 f(x)=则满足不等式 f(1-x2)>f(2x)的 x 的范围是 .【解析】画出函数 f(x)的图象,根据单调性,得,解得 x∈(-1,-1).说明:1.函数单调性是比较大小和解不等...