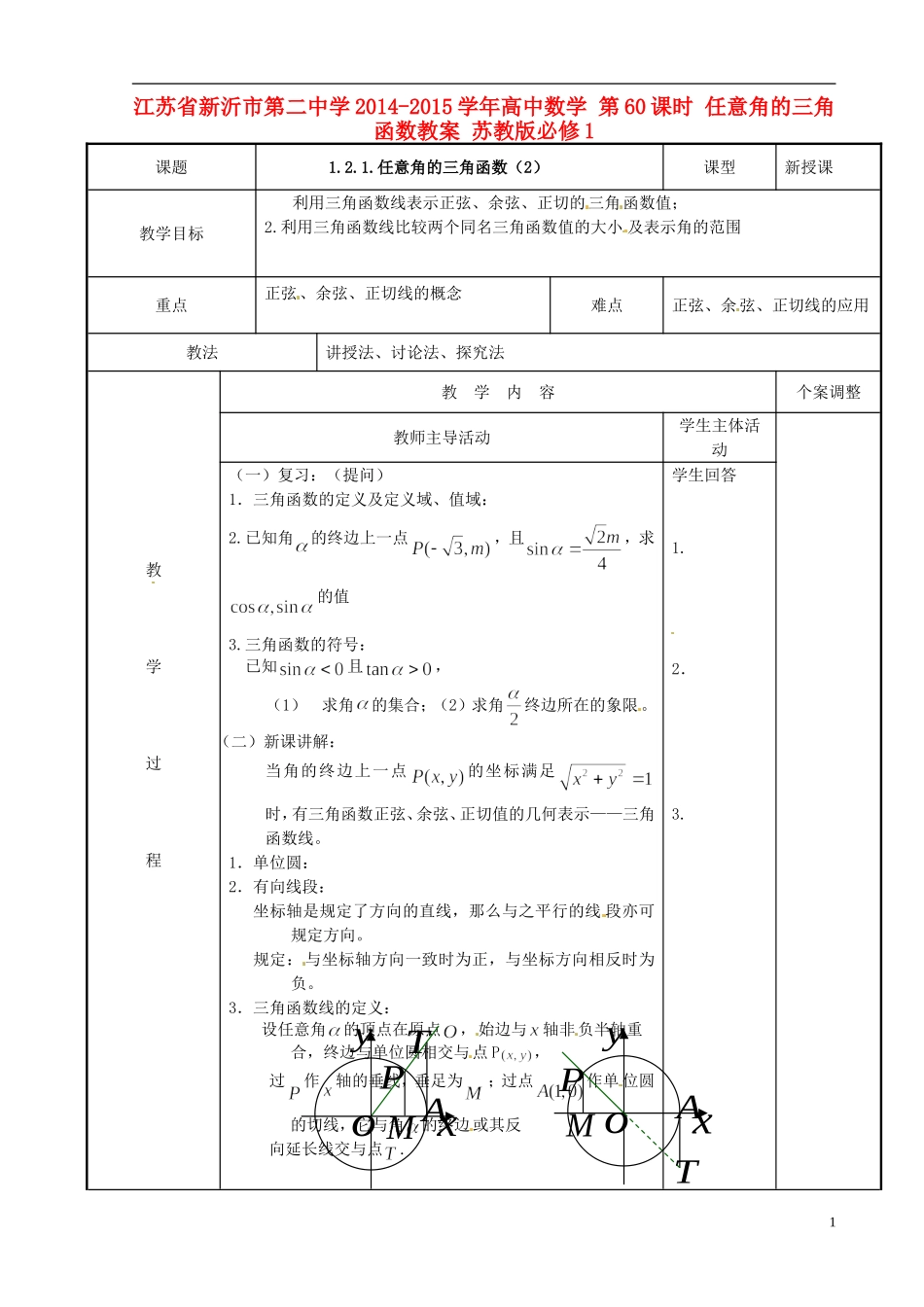
江苏省新沂市第二中学 2014-2015 学年高中数学 第 60 课时 任意角的三角函数教案 苏教版必修 1课题1.2.1.任意角的三角函数(2)课型新授课教学目标利用三角函数线表示正弦、余弦、正切的三角函数值;2.利用三角函数线比较两个同名三角函数值的大小 及表示角的范围重点正弦、余弦、正切线的概念难点正弦、余弦、正切线的应用教法讲授法、讨论法、探究法教学过程教 学 内 容 个案调整教师主导活动学生主体活动 (一)复习:(提问)1.三角函数的定义及定义域、值域:2.已知角的终边上一点,且,求的值3.三角函数的符号:已知且,(1)求角的集合;(2)求角终边所在的象限。(二)新课讲解:当角的终边上一点的坐标满足时,有三角函数正弦、余弦、正切值的几何表示——三角函数线。1.单位圆: 2.有向线段:坐标轴是规定了方向的直线,那么与之平行的线 段亦可规定方向。规定:与坐标轴方向一致时为正,与坐标方向相反时为负。3.三角函数线的定义:设任意角的顶点在原点,始边与轴非负半轴重合,终边与单位圆相交与点 P,过作轴的垂线,垂足为;过点作单 位圆的切线,它与角的终边或其反向延长线交与点.学生回答1.2.3.1oxyMTPAxyo MTPA(1) (2)(2) (4)由四个图看出:我们就分别称有向线段为正弦线、余弦线、正切线。说明:① 三条有向线段的位置:正弦线为的终边与单位圆的交点到轴的垂直线段;余弦线在轴上;正切线在过单位圆与轴正方向的交点的切线上,三条有向线段中两条在单位圆内,一条在单位圆外。② 三条有向线段的方向:正弦线由垂足指向的终边与单位圆的交点;余弦线由原点指向垂足;正切线由切点指向与的终边的交点。③ 三条有向线段的正负:三条有向线段凡与轴或轴同向的为正值,与轴或轴反向的为负值。④ 三条有向线段的书写:有向线段的起点字母在前,终点字母在后面。4.例题分析:例 1 作出下列各角的正弦线、余弦线、正切线。(1); (2); (3); (4).学生理解并能画出任意角的三角函数线学生做练习题2oxyMTPAxyoMTPA板书设计当堂作业课外作业教学札记3