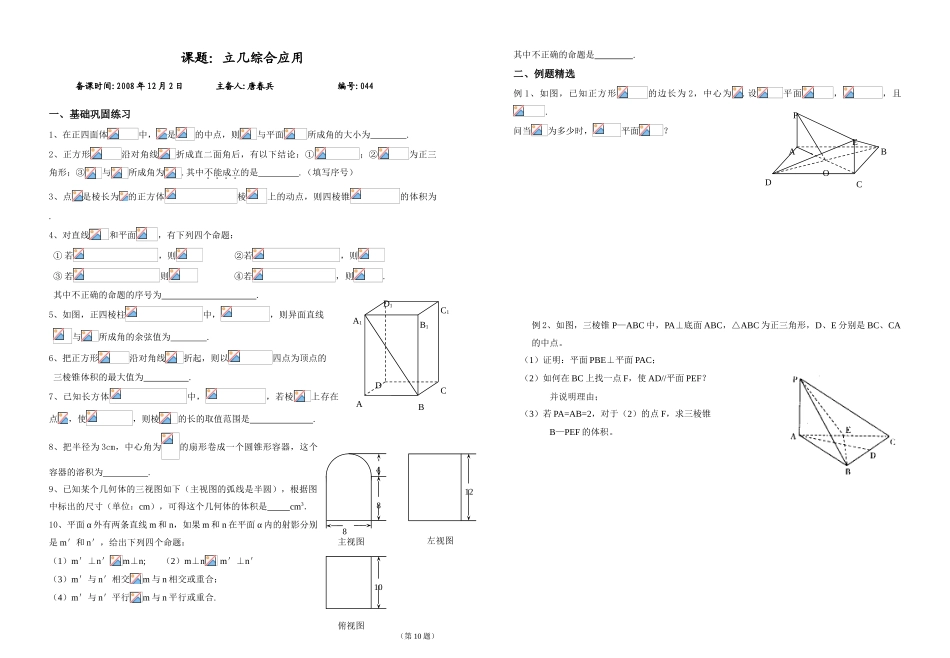
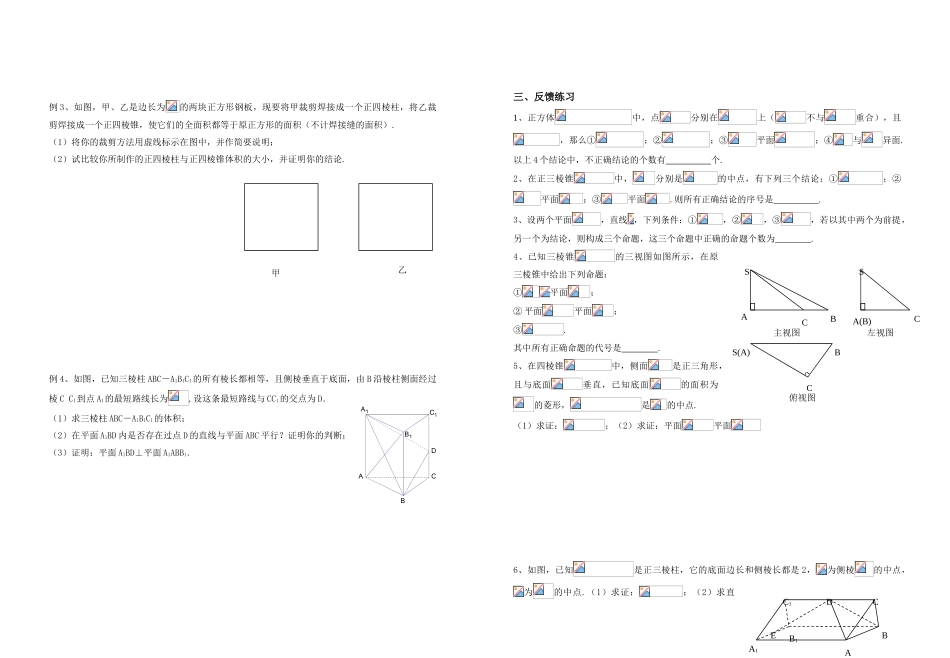
课题:立几综合应用备课时间:2008 年 12 月 2 日 主备人:唐春兵 编号:044一、基础巩固练习1、在正四面体中,是的中点,则与平面所成角的大小为 .2、正方形沿对角线折成直二面角后,有以下结论:①;②为正三角形;③与所成角为.其中不能成立的是 .(填写序号)3、点是棱长为的正方体棱上的动点,则四棱锥的体积为 .4、对直线和平面,有下列四个命题:① 若,则 ②若,则③ 若则 ④若,则.其中不正确的命题的序号为 .5、如图,正四棱柱中,,则异面直线与所成角的余弦值为 .6、把正方形沿对角线折起,则以四点为顶点的三棱锥体积的最大值为 .7、已知长方体中,,若棱上存在点,使,则棱的长的取值范围是 .8、把半径为 3cm,中心角为的扇形卷成一个圆锥形容器,这个容器的溶积为 .9、已知某个几何体的三视图如下(主视图的弧线是半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 cm3.10、平面 α 外有两条直线 m 和 n,如果 m 和 n 在平面 α 内的射影分别是 m'和 n',给出下列四个命题:(1)m'⊥n'm⊥n; (2)m⊥n m'⊥n'(3)m'与 n'相交m 与 n 相交或重合; (4)m'与 n'平行m 与 n 平行或重合.其中不正确的命题是 .二、例题精选例 1、如图,已知正方形的边长为 2,中心为.设平面,,且.问当为多少时,平面?例 2、如图,三棱锥 P—ABC 中,PA⊥底面 ABC,△ABC 为正三角形,D、E 分别是 BC、CA的中点。 (1)证明:平面 PBE⊥平面 PAC; (2)如何在 BC 上找一点 F,使 AD//平面 PEF?并说明理由; (3)若 PA=AB=2,对于(2)的点 F,求三棱锥B—PEF 的体积。ABCDA1B1C1D1左视图主视图俯视图10812(第 10 题)48ADCBEPODC1B1A1CBA例 3、如图,甲、乙是边长为的两块正方形钢板,现要将甲裁剪焊接成一个正四棱柱,将乙裁剪焊接成一个正四棱锥,使它们的全面积都等于原正方形的面积(不计焊接缝的面积).(1)将你的裁剪方法用虚线标示在图中,并作简要说明;(2)试比较你所制作的正四棱柱与正四棱锥体积的大小,并证明你的结论.例 4、如图,已知三棱柱 ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由 B 沿棱柱侧面经过棱 C C1到点 A1的最短路线长为,设这条最短路线与 CC1的交点为 D.(1)求三棱柱 ABC-A1B1C1的体积;(2)在平面 A1BD 内是否存在过点 D 的直线与平面 ABC 平行?证明你的判断;(3)证明:平面 A1B...