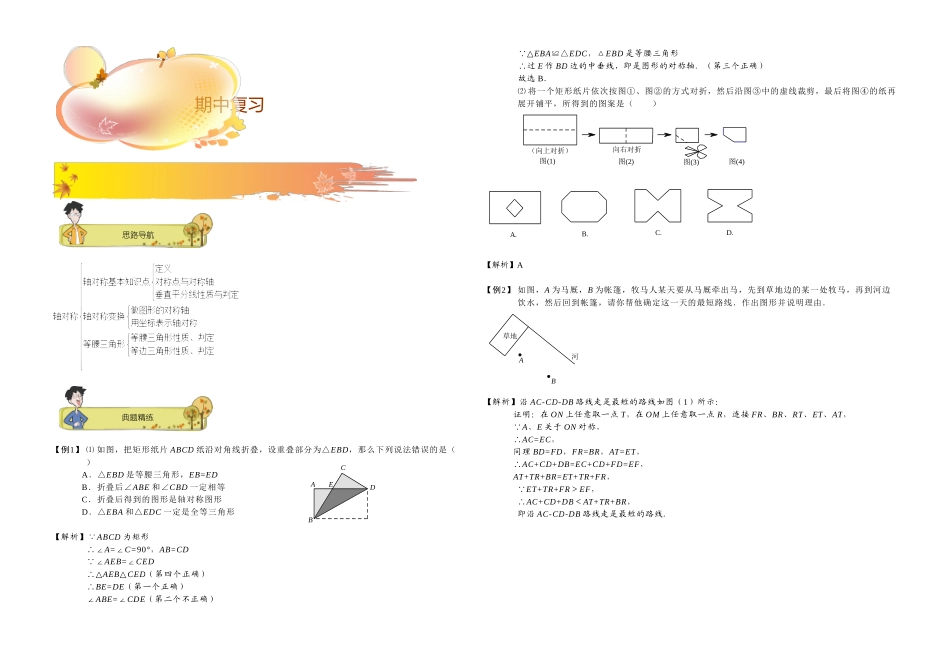
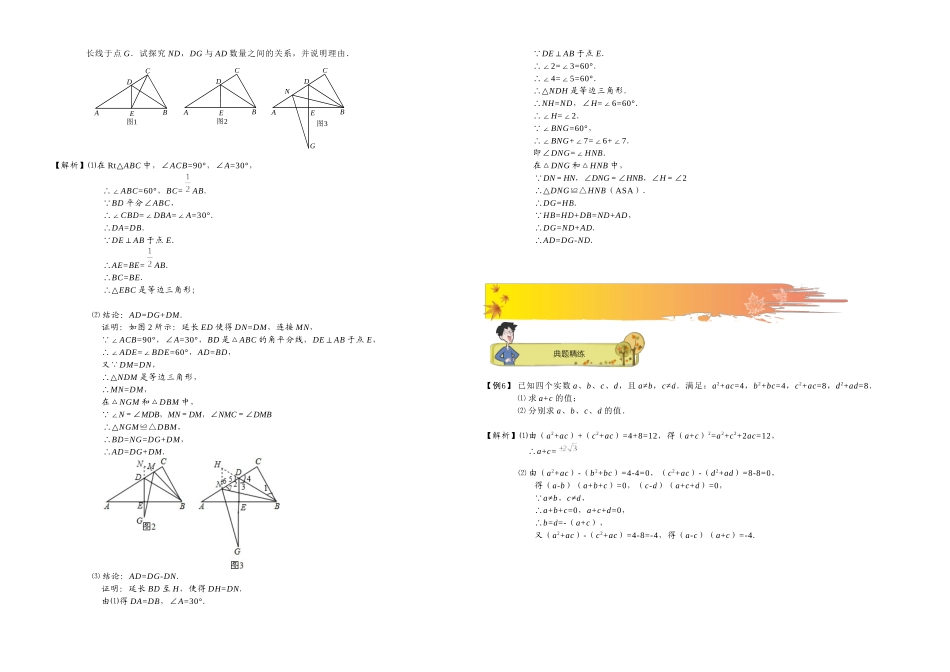
思路导航典题精练 【例1】 ⑴ 如图,把矩形纸片 ABCD 纸沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )A.△EBD 是等腰三角形,EB=EDB.折叠后∠ABE 和∠CBD 一定相等C.折叠后得到的图形是轴对称图形D.△EBA 和△EDC 一定是全等三角形【解析】 ABCD 为矩形∴∠A=∠C=90°,AB=CD ∠AEB=∠CED∴△AEB△CED(第四个正确)∴BE=DE(第一个正确)∠ABE=∠CDE(第二个不正确) △EBA≌△EDC,△EBD 是等腰三角形∴过 E 作 BD 边的中垂线,即是图形的对称轴.(第三个正确)故选 B.⑵ 将一个矩形纸片依次按图①、图②的方式对折,然后沿图③中的虚线裁剪,最后将图④的纸再展开铺平,所得到的图案是( )【解析】A【例2】 如图,A 为马厩,B 为帐篷,牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,请你帮他确定这一天的最短路线.作出图形并说明理由.【解析】沿 AC-CD-DB 路线走是最短的路线如图(1)所示:证明:在 ON 上任意取一点 T,在 OM 上任意取一点 R,连接 FR、BR、RT、ET、AT, A、E 关于 ON 对称,∴AC=EC,同理 BD=FD,FR=BR,AT=ET,∴AC+CD+DB=EC+CD+FD=EF,AT+TR+BR=ET+TR+FR, ET+TR+FR>EF,∴AC+CD+DB<AT+TR+BR,即沿 AC-CD-DB 路线走是最短的路线.题型一:轴对称7期中复习 E D C A B图(4)图(3)图(2)图(1)向右对折(向上对折)D.C.B.A.河草地 B A思路导航典题精练 【例3】 如图,在△ABC 中,BE、CF 分别是 AC、AB 两边上的高,在 BE 上截取 BD=AC,在 CF 的延长线上截取 CG=AB,连接 AD、AG.请你确定△ADG 的形状,并证明你的结论.【解析】连接 DG,则△ADG 是等腰三角形. BE、CF 分别是 AC、AB 两边上的高,∴∠AFC=∠AEB=90°∴∠ACG=∠DBA又 BD=CA,AB=GC,∴△ABD≌△GCA;∴AG=AD,∴△ADG 是等腰三角形.【例4】 △ABC 中,∠CAB=∠CBA=50°,O 为△ABC 内一点,∠OAB=10°,∠OBC=20°,求∠OCA 的度数. 【解析】作 CD⊥AB 于 D,延长 BO 交 CD 于 P,连接 PA, ∠CAB=∠CBA=50°,∴AC=BC,∴AD=BD, ∠CAB=∠CBA=50°,∴∠ACB=80°, ∠ABC=∠ACB=50°,∠OBC=20°,∴∠CBP=∠OBC=20°=∠CAP,∠PAO=∠CAB-∠CAP-∠OAB=50°-20°-10°=20°=∠CAP,∠POA=∠OBA+∠OAB=10°+50°-20°=40°=∠ACD, 在△CAP 和△OAP 中, ∠ACP=∠AOP,∠CAP=∠OAP∴△CAP≌...