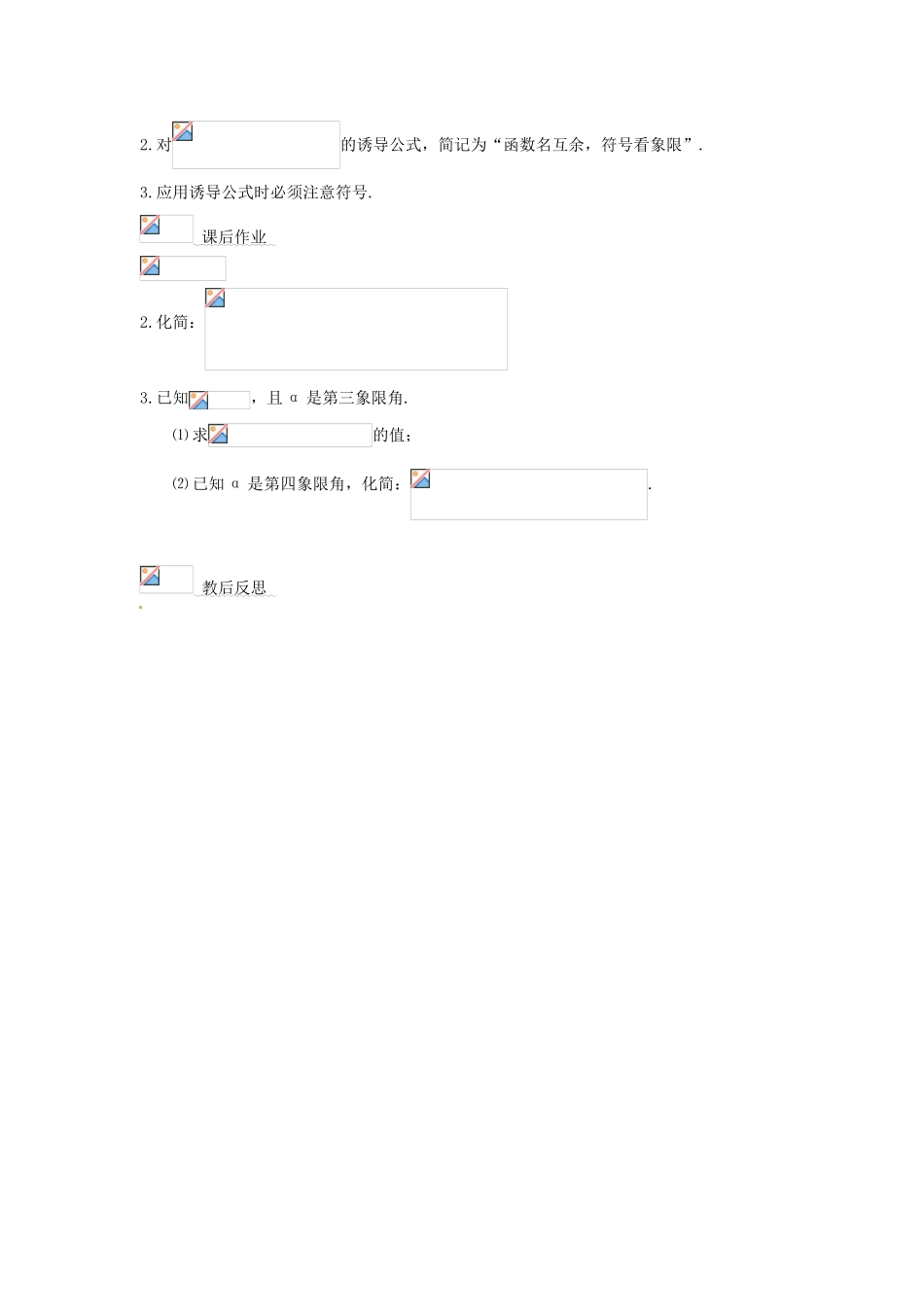
甘肃省永昌县第一中学高一数学:§1.3 三角函数的诱导公式 学习目标 1.掌握诱导公式一到六,掌握这三种形式的角的三角函数与角三角函数间的关系.2.利用诱导公式求三角函数值、化简、证明恒等式. 学习重点 理解和掌握诱导公式. 学习难点 对诱导公式的熟练运用. 教学设计 一、展示目标二、自主学习复习 1、角 α 的终边与单位圆交于点 P(x, y),则:sinα= ;cosα= ;tanα= 。复习 2、诱导公式(一)sin(2 kπ+)= ; cos(2 kπ+)= ;tg(2 kπ+)= 。此公式将任意范围内的角的三角函数值转化到 0~2π 后,又如何将 0~2π 间的角转化到 0~呢?(自学教材 P23~ P26,找出疑惑之处)三、合作探究新知:诱导公式( 二)sin(π+α)= ;cos(π+α) = ;tan(π+α) = 。诱导公式(三)sin(-α)= ;cos(-α) = ;tan(-α) = 。诱导公式(四)sin(π-α)= ;cos(π-α) = ;tan(π-α) = 。记忆口诀:函数名不变,符号看象限。探究任务二:的诱导公式新知:诱导公式(五) ; 。诱导公式(六) ; 。六组诱导公式都可统一为“”的形式,记忆的口诀为“奇变偶不变,符号看象限”。四、精讲点拨例 1、求 值:(1)sin240°,(2)cos,(3) sin(-),(4)cos(—210°)例 2、化简:。例 3、证明:(1),(2)。五、达标检测1、的值为( ) A. B. C. D.2、的值等于( ) A. B. C. D.3、下列各式不正确的是( )A. sin(+180°)=-sinα B. B.cos(-+β)=-cos(-β)C. sin(--360°)=-sinα D.cos(--β)=cos(+β)4、已知,计算:六、课堂小结1.应用诱导公式求三角函数值时的一般步骤为:负角化正角→大角化小角→查表求值2.对的诱导公式,简记为“函数名互余,符号看象限”.3.应用诱导公式时必须注意符号. 课后作业 2.化简:3.已知,且 α 是第三象限角.⑴ 求的值;⑵ 已知 α 是第四象限角,化简:. 教后反思