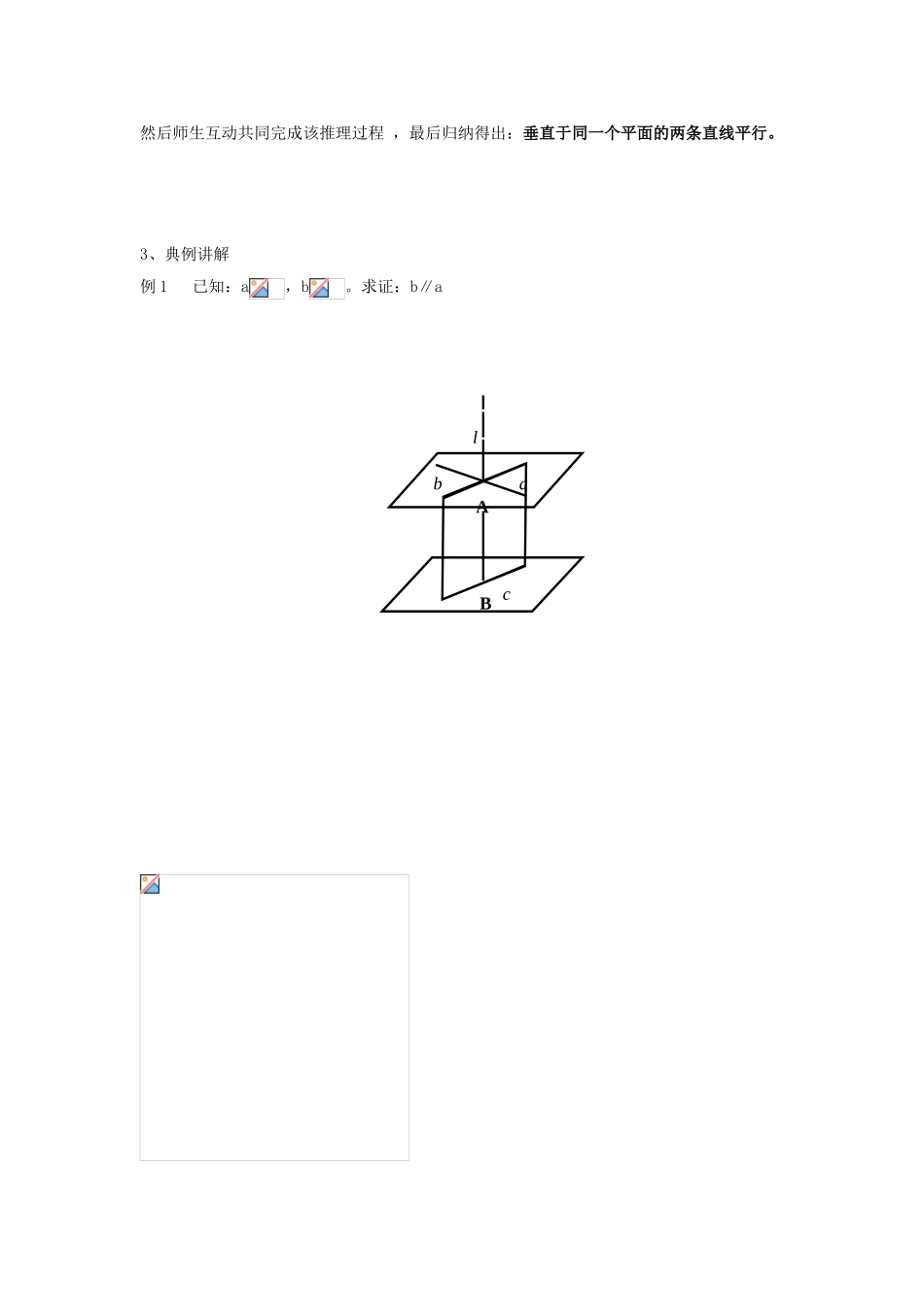
甘肃省永昌县第一中学高中数学 2、3.3 直线与平面垂直的性质、平面与平面垂直的性质学案 新人教 A 版必修 2学习目标:1 使学生掌握直线与平面垂直,平面与平面垂直的性质定理;2 能运用性质定理解决一些简单问题;3 了解直线与平面、平面与平面垂直的判定定理和性质定理间的相互联系。学习重点、难点两个性质定理的证明。学习过程一、展示目标二、自主学习 问题:若一条直线与一个平面垂直,则可得到什么结论?若两条直线与同一个平面垂直呢?让学生自主学习,教师不急于下结论,而是继续引导学生:欲知结论怎样,让我们一起来观察、研探。(自然进入课题内容)三、交流互动1、操作确认观察长方体模型中四条侧棱与同一个底面的位置关系。如图 2.3—4,在长方体中,棱所在直线都垂直于平面,它们之间是有什么位置关系?(显然互相平行)然后 进一步迁移活动:已知直线、那么直线一定平行吗?(一定)我们能否证明这一事实的正确性呢?2、推理证明引导学生分析性质定理成立的条件,介绍证明性质定理成立的特殊方法——反证法, 然后师生互动共同完成该推理过程 ,最后归纳得出:垂直于同一个平面的两条直线平行。3、典例讲解例 1 已知:a,b。求证:b∥aablAB c四、达标检测 1.若表示直线,表示平面,下列条件中,能使的是 ( ) 2.已知 与是两条不同的直线,若直线平面,①若直线,则;②若,则;③若,则;④,则。上述判断正确的是 ( )①②③ ②③④ ①③④ ②④3.下列关于直线与平面的命题中,真命题是 ( )若且,则 若且,则若且,则 且,则五、归纳总结(1)请归纳一下本节学习了什么性质定理,其内容各是什么? (2)类比两个性质定理,你发现它们之间有何联系?六、作业布置1 求证:两条异面直线不能同时和一个平面垂直; 2 求证:三个两两垂直的平面的交线两两垂直。七、课后反思