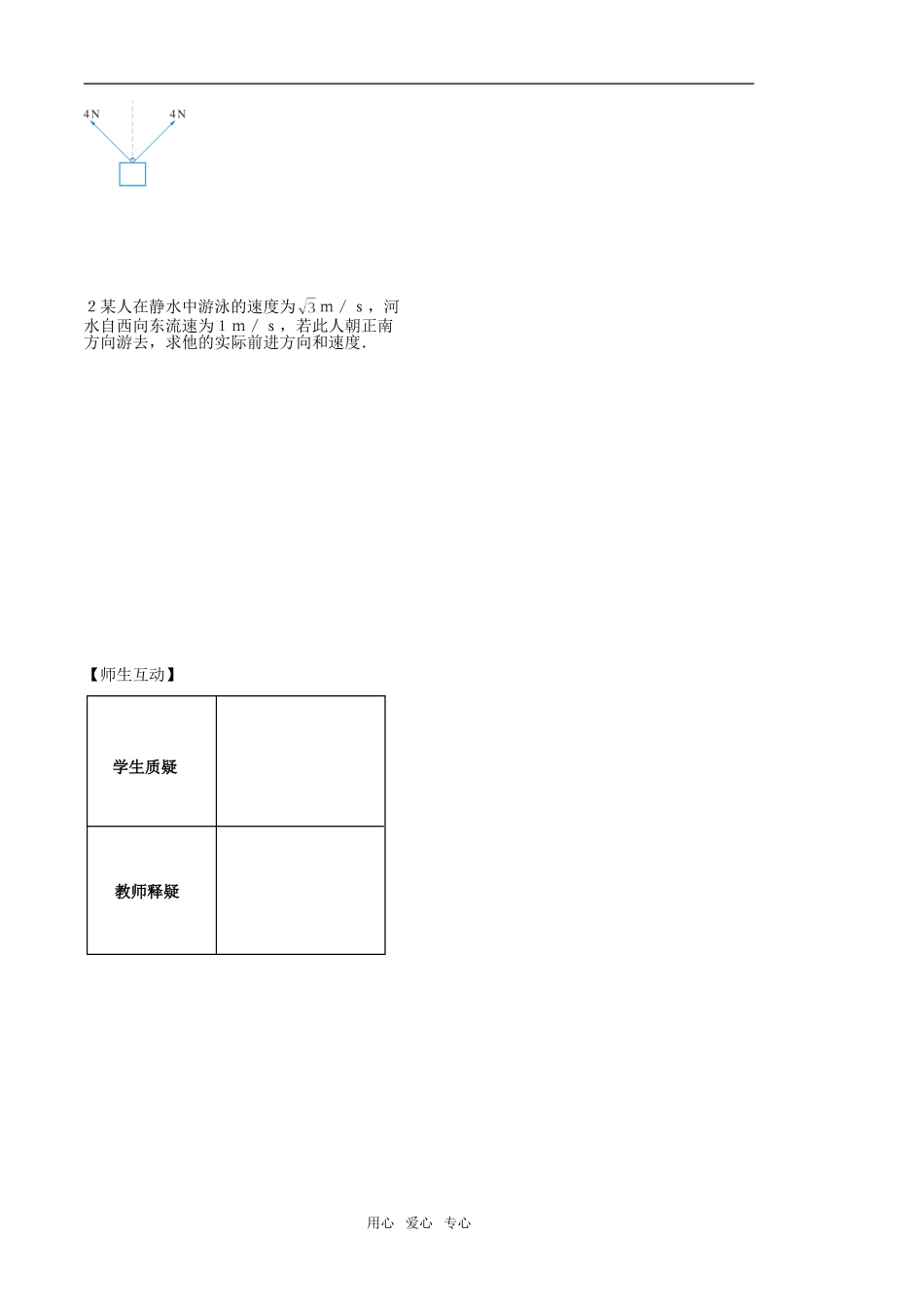
2.5 向量的应用【学习导航】知识网络矢量的合成物理问题 矢量的分解向量的应用数学问题 几何问题学习要求 1.经历用向量方法解决某些简单的几何问题,力学问题的思想方法,体会向量是一种重要的数学工具。2.通过问题的解决培养学生运算能力和解决实际问题的能力。【课堂互动】自学评价1.力、_________________位移等都是向量;2.力、速度、加速度、位移的合成与分解就是向量的__________,运动的叠加也用到向量的合成;3.功就是力与所产生的位移的___________【精典范例】一、向量在物理中的应用例 1 如图 (1)所示,无弹性的细绳 OA,OB 的一端分别固定在 A,B 处,同质量的细绳 OC 下端系着一个称盘,且使得 OB⊥OC,试分析OA,OB,OC 三根绳子受力的大小,判断哪根绳受力最大。【解】 用心 爱心 专心听课随笔归纳研究:① 利用向量解决物理问题,首先要用向量来表示问题中的物理关系,建立相应的数学模型,然后进行向量的计算得出结果。根据结果对相关的物理关系作出解释。② 物理中的受力分析,速度分解等一般都可以用向量来解决。二、向量在平面几何中的应用例2 已知:⊥,⊥求证:.【证明】 归纳总结:① 能否用一个几何图形来解释例 2 ?在△ABC 中,OA⊥BC, OB⊥AC,则 OC⊥AB 。这几个几何现象表示为三角形的三条高交于一点 O,这个 O 点就是△ABC 的垂心。这个向量方法的证明比平面几何方法的证明要简捷。②事实上,许多平面几何问题都能用向量方法证明。我们可以引入向量,通过向量的运算来证明。同学可举例尝试证明,如在直角三角形中某些性质:勾股定理、斜线上中线定理等。三、向量在解析几何中的应用例 3 已 知 直 线 l 经 过 点和,用向量方法求 l 的方程.分析:设 P 是直线 l 上任意一点,由与共线的条件可推得直线 l 的方程.【解】 追踪训练一1.如图,一个三角形角铁支架ABC安装在墙壁上,AB∶AC∶BC=3∶4∶5,在B处挂一个6kg的物体,求角铁AB与BC所受的力.2.用向量方法证明梯形中位线定理.3.直线 l 平行于向量a=(2,3),求直线 l 的斜率.4.直线 l 经过原点且与向量a=(2,3)垂直,求直线 l 的方程.追踪训练二1 如图,夹角为90°的两根绳子提起一个重物,每根绳子用力4N,求物体的重量.用心 爱心 专心听课随笔2某人在静水中游泳的速度为m/s,河水自西向东流速为1m/s,若此人朝正南方向游去,求他的实际前进方向和速度.【师生互动】用心 爱心 专心学生质疑教师释疑