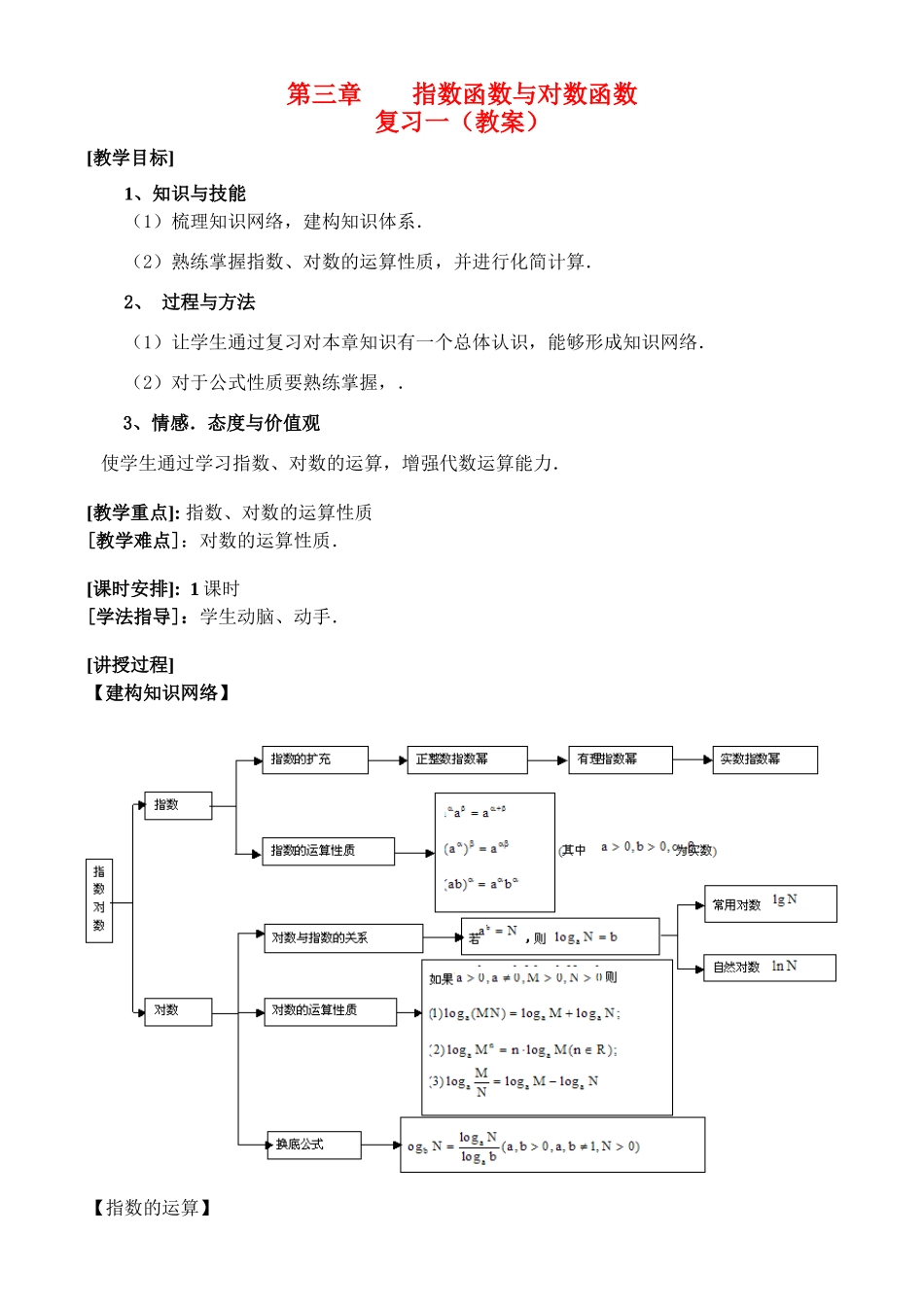
第三章 指数函数与对数函数 复习一(教案)[教学目标]1、知识与技能 (1)梳理知识网络,建构知识体系.(2)熟练掌握指数、对数的运算性质,并进行化简计算. 2、 过程与方法 (1)让学生通过复习对本章知识有一个总体认识,能够形成知识网络.(2)对于公式性质要熟练掌握,. 3、情感.态度与价值观 使学生通过学习指数、对数的运算,增强代数运算能力.[教学重点]: 指数、对数的运算性质[教学难点]:对数的运算性质.[课时安排]: 1 课时[学法指导]:学生动脑、动手.[讲授过程] 【建构知识网络】 【指数的运算】例 1.计算下列各式(式子中字母都是正数):(1)(2)(-6)÷(-3); (2)(解:(1)(2)(-6)÷(-3) =[2×(-6)÷(-3)] =4a (2)(=(练习 1:计算下列各式(式子中字母都是正数):; 【根式的运算】例 2.计算下列各式:(1); (2)(a>0)解:(1)==-5(2)(a>0)==练习 2:.计算下列各式:;【对数的运算】例 3.计算:log(3+2)的值.解:log(3+2)=例 4.已知 lgx = a,lgy = b,lgz = c,且有 a+b+c = 0,求 x·y·x的值.解:.由 lgx = a,lgy = b,lgz = c,得 x = 10 ,y = 10 ,z = 10 ,所以 x·y·x=10=10= 0=.练习 3:(1).已知 log [ log( log x)] = log [ log( log y)] = log [ log( log z)] = 0,试比较 x、y、z 的大小.解:由 log [ log( log x)] = 0 得,log( log x)= 1,log x =,即 x = 2;由 log [ log( log y)] = 0 得,log( log y) = 1,log y =,即 y =3 ;由 log [ log( log z)] = 0 得,log( log z) = 1,log z =,即 z = 5 .∵y =3 = 3= 9,∴x = 2= 2= 8,∴y>x,又∵x = 2= 2= 32,z = 5 = 5= 25,∴x>z.故 y>x>z.(2).设 a,b 为正数,且 a -2ab-9b = 0,求 lg(a +ab-6b )-lg(a +4ab+15b )的值.解:由 a -2ab-9b = 0,得() -2()-9 = 0,令= x>0,∴x -2x-9 = 0,解得 x =1+,(舍去负根),且 x = 2x+9,∴lg(a +ab-6b )-lg(a +4ab+15b ) = lg= lg= lg= lg= lg= lg= lg=-.作业:复习题三 A 组 1-4