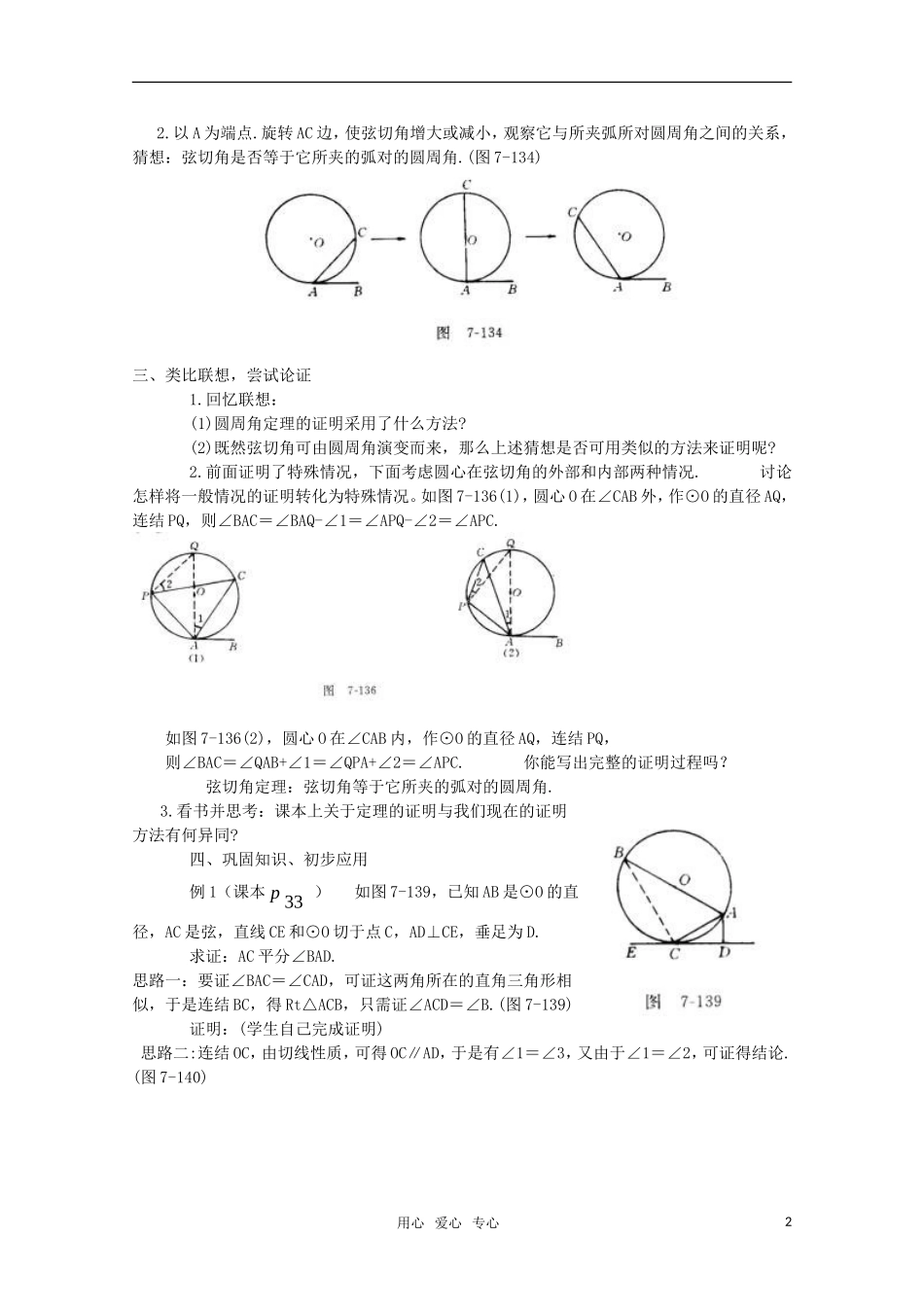
高二数学选修 4-1 学案弦切角的性质班级 姓名 学号学习目标:1.理解弦切角的概念;2.掌握弦切角定理及推论,并会运用它们解决有关问题;3.理解化归和分类讨论的数学思想方法以及完全归纳的证明方法.教学重点和难点弦切角定理及其应用是重点; 弦切角定理的证明是难点.教学过程:一、创设情境,以旧探新 1.提问:什么样的角是圆周角? 2.圆周角∠CAB,让射线 AC 绕点 A 旋转,产生无数个圆周角,当 AC 绕点 A 旋转至与圆相切时,停止旋转,得∠BAE.(图 7-132) 思考:这时∠BAE 还是圆周角吗?为什么? 归纳总结出弦切角的特点: (1)顶点在圆周上; (2)一边与圆相交; (3)一边与圆相切. 3. 弦切角定义: 顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角. 4.判断下列各图形中的角是不是弦切角,并说明理由: (图 7-133) [来源:高考%资源网 KS%5U] 由此发现,弦切角可分为三类:(1)圆心在角的外部; (2)圆心在角的一边上; (3)圆心在角的内部. 二、观察联想、发现规律1.当弦切角一边通过圆心时,(如图 7-135) (1)弦切角∠CAB 是多少度?为什么? (2)∠CAB 所夹弧所对的圆周角∠D 是多少度?为什么? (3)此时,弦切角与它所夹弧所对的圆周角有什么关系?观察图形,不难发现,此时弦切角与其所夹弧所对的圆周角都是直角.用心 爱心 专心1 2.以 A 为端点.旋转 AC 边,使弦切角增大或减小,观察它与所夹弧所对圆周角之间的关系,猜想:弦切角是否等于它所夹的弧对的圆周角.(图 7-134) 三、类比联想,尝试论证 1.回忆联想: (1)圆周角定理的证明采用了什么方法? (2)既然弦切角可由圆周角演变而来,那么上述猜想是否可用类似的方法来证明呢? 2.前面证明了特殊情况,下面考虑圆心在弦切角的外部和内部两种情况. 讨论怎样将一般情况的证明转化为特殊情况。如图 7-136(1),圆心 O 在∠CAB 外,作⊙O 的直径 AQ,连结 PQ,则∠BAC=∠BAQ-∠1=∠APQ-∠2=∠APC.如图 7-136(2),圆心 O 在∠CAB 内,作⊙O 的直径 AQ,连结 PQ,则∠BAC=∠QAB+∠1=∠QPA+∠2=∠APC. 你能写出完整的证明过程吗? 弦切角定理:弦切角等于它所夹的弧对的圆周角.3.看书并思考:课本上关于定理的证明与我们现在的证明方法有何异同? 四、巩固知识、初步应用 例 1(课本33p) 如图 7-139,已知 AB 是⊙O 的直径,AC 是弦,直线 CE 和⊙O 切于点 C,AD⊥CE,垂足为 D. 求证:AC 平分∠BAD.思路...