高二数学上学期期末复习备考讲练 专题06 圆锥曲线与方程导学案 理-人教版高二全册数学学案

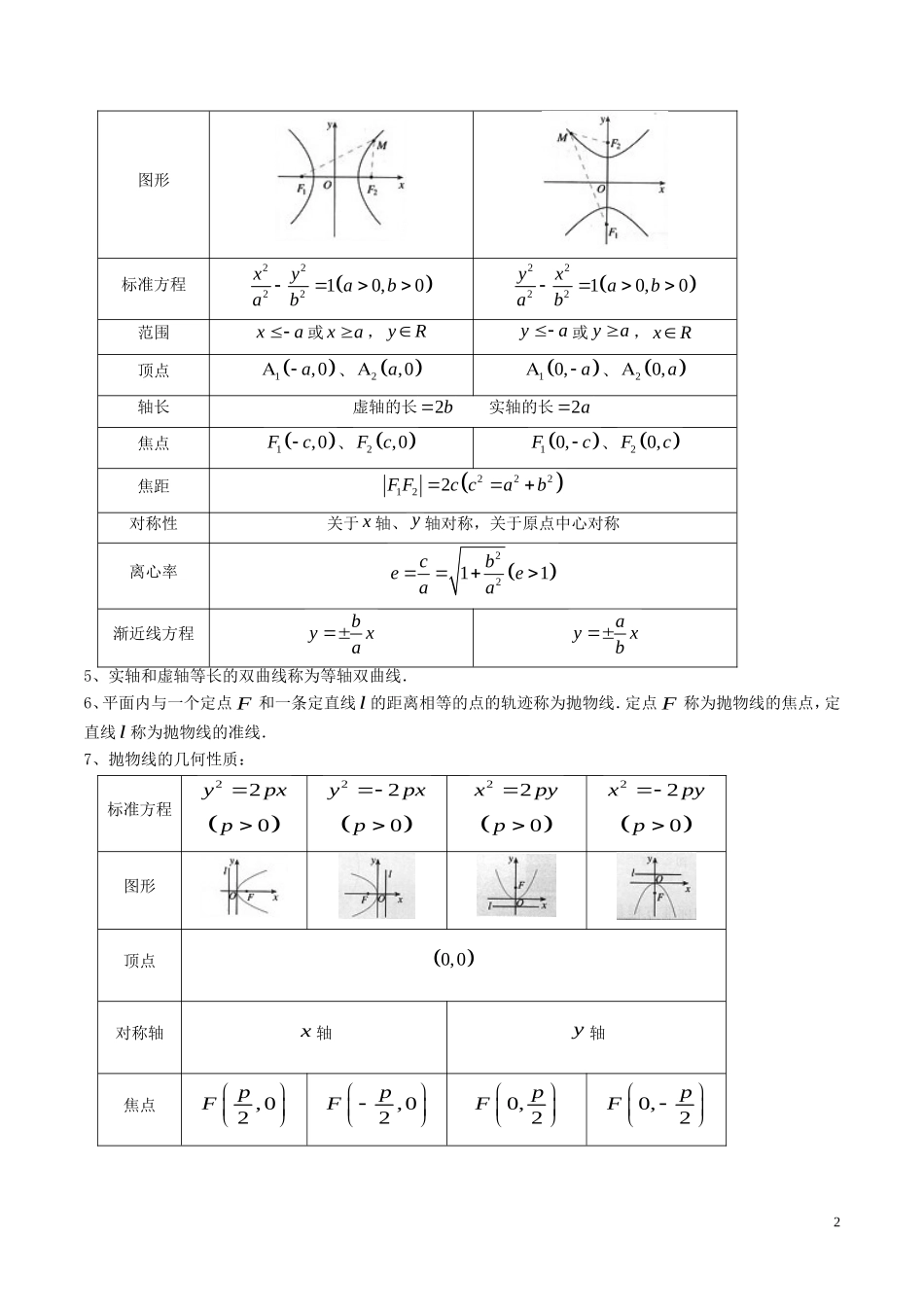
专题 06 圆锥曲线与方程一、学习目标：1.了解圆锥曲线的实际背景，了解圆锥曲线在刻画现实世界和解决实际问题中的作用.2.掌握椭圆、抛物线的定义、几何图形、标准方程及简单性质.3.了解双曲线的定义、几何图形和标准方程，知道它的简单几何性质.4.了解圆锥曲线的简单应用.5.理解数形结合的思想.二、知识梳理1、平面内与两个定点1F ，2F 的距离之和等于常数（大于12F F）的点的轨迹称为椭圆．即：|)|2(,2||||2121FFaaMFMF。这两个定点称为椭圆的焦点，两焦点的距离称为椭圆的焦距．2、椭圆的几何性质：焦点的位置焦点在 x 轴上焦点在 y 轴上图形标准方程222210xyabab222210yxabab范围axa  且 byb bxb  且 aya 顶点1,0a 、2,0a1 0, b、2 0,b1 0, a、2 0,a1,0b、2,0b轴长短轴的长2b 长轴的长2a焦点1,0Fc、2,0Fc1 0,Fc、2 0,Fc焦距222122F Fc cab对称性关于 x 轴、 y 轴、原点对称离心率22101cbeeaa3、平面内与两个定点1F ，2F 的距离之差的绝对值等于常数（小于12F F）的点的轨迹称为双曲线．即：|)|2(,2||||||2121FFaaMFMF。这两个定点称为双曲线的焦点，两焦点的距离称为双曲线的焦距．4、双曲线的几何性质：焦点的位置焦点在 x 轴上焦点在 y 轴上1图形标准方程222210,0xyabab222210,0yxabab范围xa或 xa ， yRya或 ya， xR顶点1,0a 、2,0a1 0, a、2 0,a轴长虚轴的长2b 实轴的长2a焦点1,0Fc、2,0Fc1 0,Fc、2 0,Fc焦距222122F Fc cab对称性关于 x 轴、 y 轴对称，关于原点中心对称离心率2211cbeeaa渐近线方程byxaayxb5、实轴和虚轴等长的双曲线称为等轴双曲线．6、平面内与一个定点 F 和一条定直线l 的距离相等的点的轨迹称为抛物线．定点 F 称为抛物线的焦点，定直线l 称为抛物线的准线．7、抛物线的几何性质：标准方程22ypx0p 22ypx0p 22xpy0p 22xpy0p 图形顶点0,0对称轴x 轴y 轴焦点,02pF ,02pF 0, 2pF 0,2pF 2准线方程2px 2px 2py 2py 离心率1...