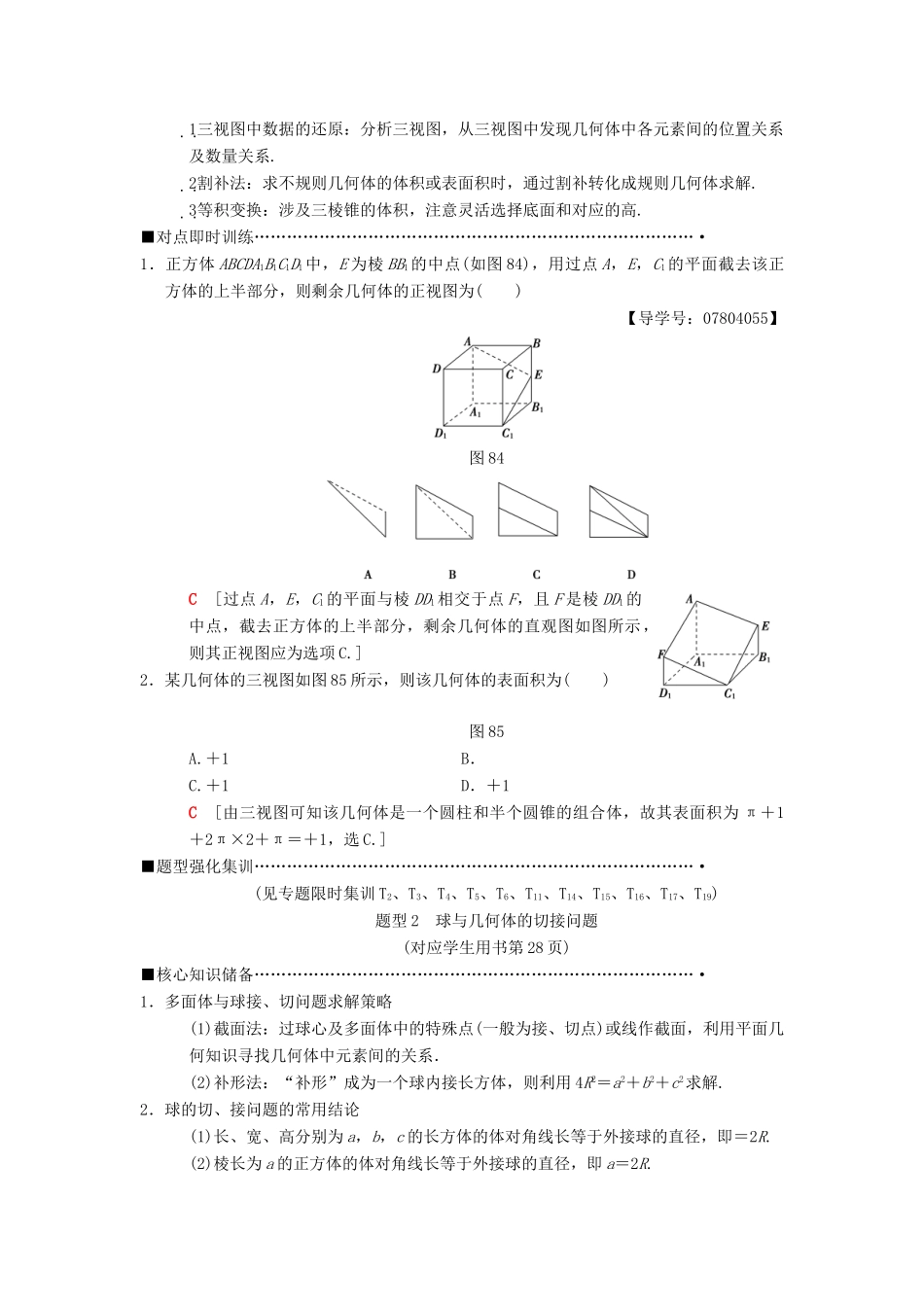
第 8 讲 空间几何体的三视图、表面积和体积题型 1 几何体的三视图、表面积和体积(对应学生用书第 27 页)■核心知识储备………………………………………………………………………·1.画几何体的三视图应遵循:“长对正、高平齐、宽相等”.2.柱体、锥体、台体的侧面积公式(1)S 柱侧=ch(c 为底面周长,h 为高);(2)S 锥侧=ch′(c 为底面周长,h′为斜高);(3)S 台侧=(c+c′)h′(c′,c 分别为上下底面的周长,h′为斜高).3.柱体、锥体、台体的体积公式(1)V 柱体=Sh(S 为底面面积,h 为高);(2)V 锥体=Sh(S 为底面面积,h 为高);(3)V 台=(S++S′)h(不要求记忆).4.球体的体积公式V=πR3;表面积公式 S=4πR2(其中 R 为球的半径).■典题试解寻法………………………………………………………………………·【典题 1】 (考查多面体的体积问题)如图 81,网格纸上小正方形的边长为 1,粗实线画出的是某多面体的三视图,则该多面体的体积为( ) 【导学号:07804054】图 81A.64 B. C.16 D.[思路分析] 三视图―→直观图―→多面体的体积.[解析] 利用正方体还原几何体,如图中的三棱锥 DABC 所示,由三视图可知△ABC 的边 BC=2,BC 边上的高为 4,三棱锥 DABC 的高为 CD=4,故三棱锥 DABC 的体积为 V=××2×4×4=.故选 D.[答案] D【典题 2】 (考查组合体的表面积问题)(2016·全国Ⅰ卷)如图 82,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是( )图 82A.17π B.18πC.20πD.28π[思路分析] 三视图―→球体的―→球体的半径―→几何体的表面积.[解析] 由几何体的三视图可知,该几何体是一个球体去掉上半球的,得到的几何体如图.设球的半径为 R,则 πR3-×πR3=π,解得 R=2.因此它的表面积为×4πR2+πR2=17π.故选 A.[答案] A【典题 3】 (考查立体几何中的数学文化题)(2017·武昌区模拟)(立体几何中的数学文化题)中国古代数学名著《九章算术》中记载了公元前 344 年商鞅监制的一种标准量器——商鞅铜方升,其三视图如图 83 所示(单位:寸),若 π 取 3,其体积为 12.6(单位:立方寸),则图中的 x 为( )图 83A.1.2B.1.6C.1.8D.2.4[思路分析] 数学文化信息提取―→空间几何体的体积―→量的计算.[解析] 该几何体是一个组合体,左边是一个底面半径为的圆柱,右边是一个长、宽、...