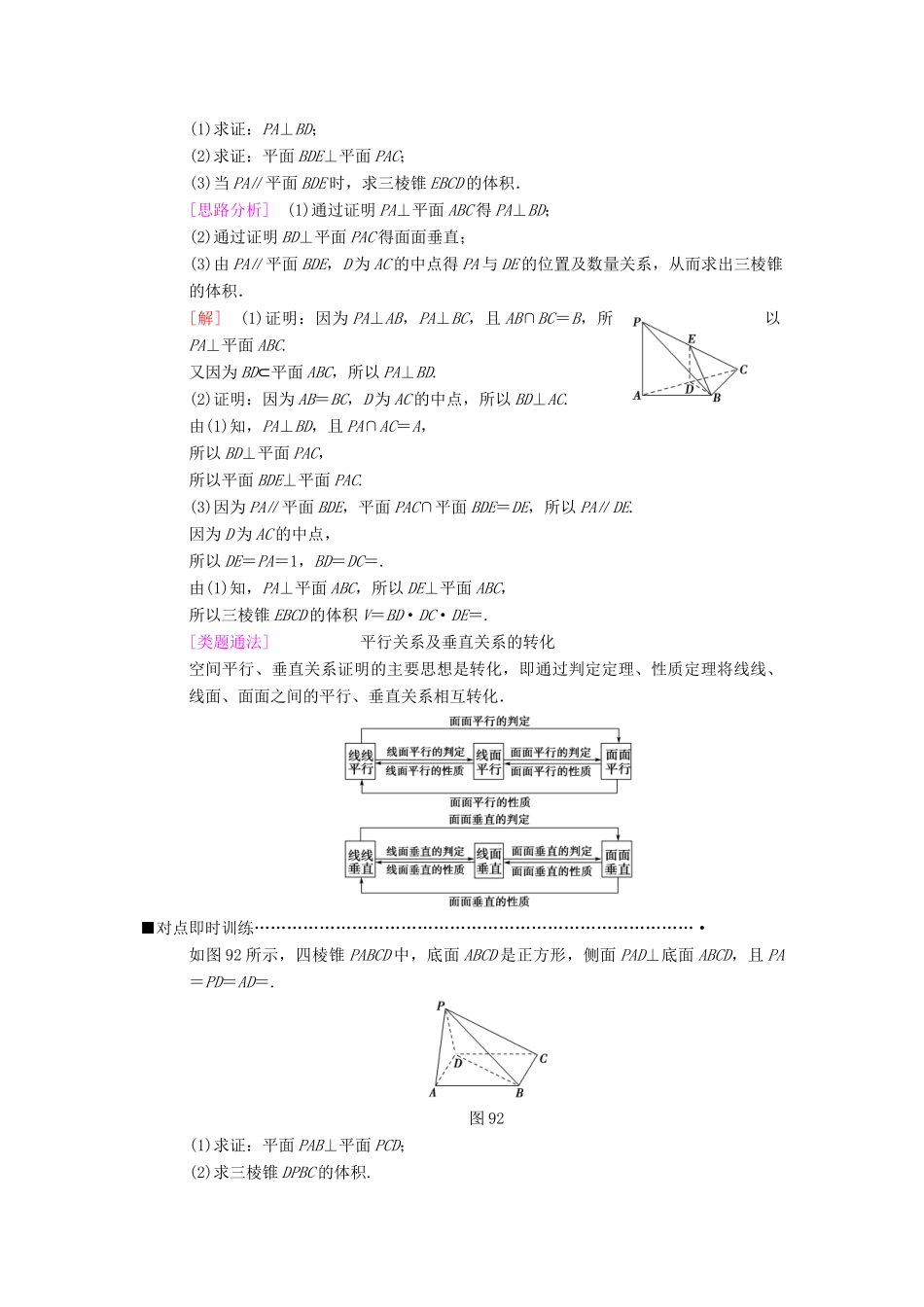
第 9 讲 空间中的平行与垂直关系题型 1 空间位置关系的判断与证明(对应学生用书第 30 页)■核心知识储备………………………………………………………………………·1.直线、平面平行的判定及其性质(1)线面平行的判定定理:a⊄α,b⊂α,a∥b⇒a∥α.(2)线面平行的性质定理:a∥α,a⊂β,α∩β=b⇒a∥b.(3)面面平行的判定定理:a⊂β,b⊂β,a∩b=P,a∥α,b∥α⇒α∥β.(4)面面平行的性质定理:α∥β,α∩γ=a,β∩γ=b⇒a∥b.2.直线、平面垂直的判定及其性质(1)线面垂直的判定定理:m⊂α,n⊂α,m∩n=P,l⊥m,l⊥n⇒l⊥α.(2)线面垂直的性质定理:a⊥α,b⊥α⇒a∥b.(3)面面垂直的判定定理:a⊂β,a⊥α⇒α⊥β.(4)面面垂直的性质定理:α⊥β,α∩β=l,a⊂α,a⊥l⇒a⊥β.■典题试解寻法………………………………………………………………………·【典题 1】 (考查空间位置关系的判断)已知 m,n 为异面直线,m⊥平面 α,n⊥平面 β.直线 l 满足 l⊥m,l⊥n,l⊄α,l⊄β,则( )A.α∥β 且 l∥αB.α⊥β 且 l⊥βC.α 与 β 相交,且交线垂直于 lD.α 与 β 相交,且交线平行于 l[解析] 根据所给的已知条件作图,如图所示.由图可知 α 与 β 相交,且交线平行于 l,故选 D.[答案] D【 典 题 2 】 ( 考 查 空 间 位 置 关 系 的 证 明 ) 如 图 91 , 在 三 棱 锥 PABC 中 ,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D 为线段 AC 的中点,E 为线段 PC 上一点.图 91(1)求证:PA⊥BD;(2)求证:平面 BDE⊥平面 PAC;(3)当 PA∥平面 BDE 时,求三棱锥 EBCD 的体积.[思路分析] (1)通过证明 PA⊥平面 ABC 得 PA⊥BD;(2)通过证明 BD⊥平面 PAC 得面面垂直;(3)由 PA∥平面 BDE,D 为 AC 的中点得 PA 与 DE 的位置及数量关系,从而求出三棱锥的体积.[解] (1)证明:因为 PA⊥AB,PA⊥BC,且 AB∩BC=B,所以PA⊥平面 ABC.又因为 BD⊂平面 ABC,所以 PA⊥BD.(2)证明:因为 AB=BC,D 为 AC 的中点,所以 BD⊥AC.由(1)知,PA⊥BD,且 PA∩AC=A,所以 BD⊥平面 PAC,所以平面 BDE⊥平面 PAC.(3)因为 PA∥平面 BDE,平面 PAC∩平面 BDE=DE,所以 PA∥DE.因为 D 为 AC 的中点,所以 DE=PA=1,BD=DC=.由(1)知,PA⊥平面 ABC,所以 DE⊥平面 ABC,所以三棱锥 EBCD 的体积 V=BD...