高考数学二轮复习 专题二 第1讲 三角函数学案-人教版高三全册数学学案

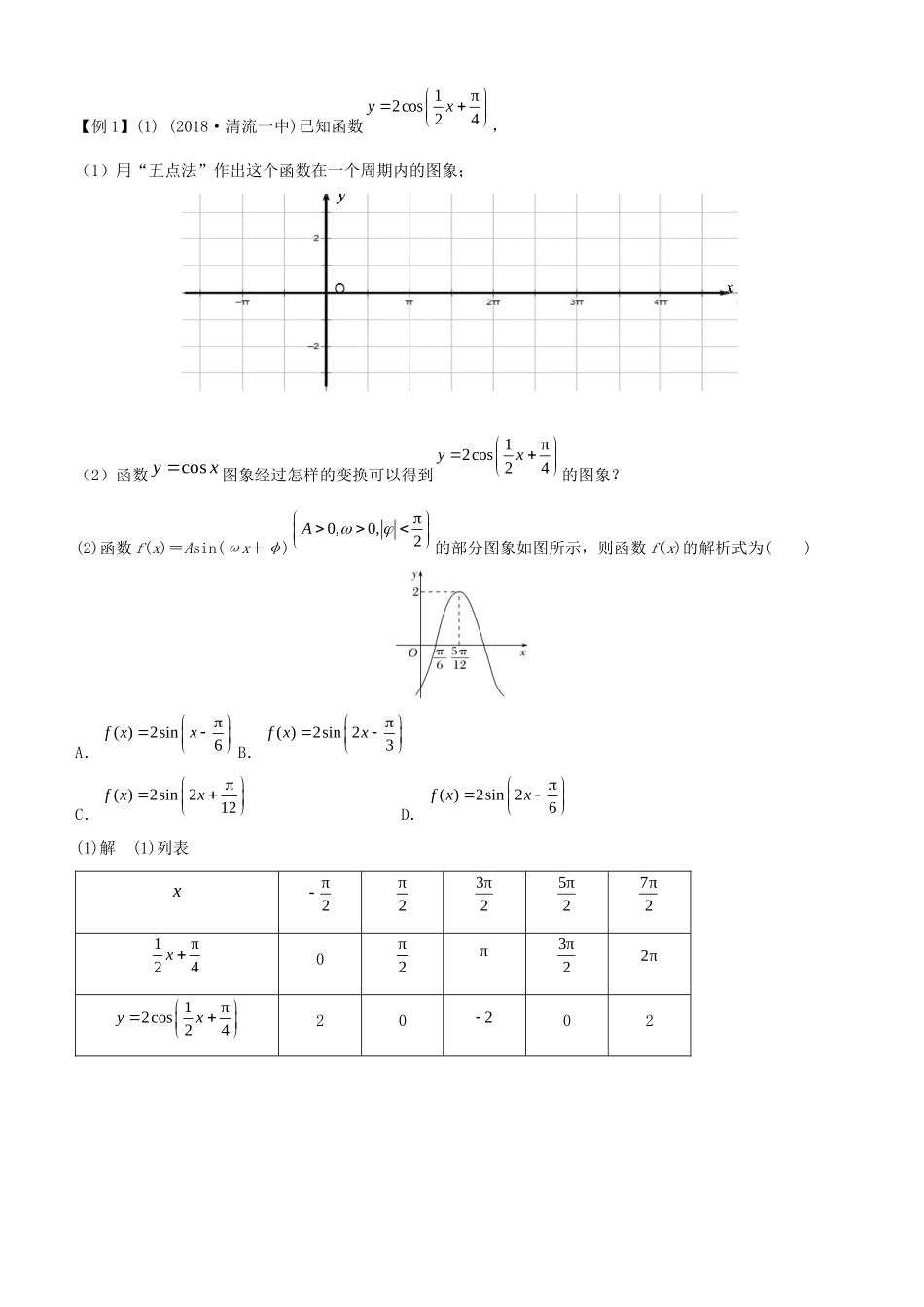
第 1 讲三角函数1．三角函数的图象，主要涉及图象变换问题以及由图象确定解析式问题，主要以选择题、填空题的形式考查；2．利用三角函数的性质求解三角函数的值、参数、最值、值域、单调区间等，主要以解答题的形式考查；3．三角函数的化简与求值是高考的命题热点，其中同角三角函数的基本关系、诱导公式是解决计算问题的工具，三角恒等变换是利用三角恒等式(两角和与差、二倍角的正弦、余弦、正切公式)进行变换，“角”的变换是三角恒等变换的核心．1．常用三种函数的图象性质(下表中)函数y＝sin xy＝cos xy＝tan x图象递增区间递减区间奇偶性奇函数偶函数奇函数对称中心对称轴x＝kπ＋x＝kπ周期性2π2ππ2．三角函数的常用结论(1)y＝Asin(ωx＋φ)，当 φ＝kπ(k∈Z)时为奇函数；当 φ＝kπ＋()时为偶函数；对称轴方程可由 ωx＋φ＝kπ＋()求得．(2)y＝Acos(ωx＋φ)，当 φ＝kπ＋(k∈Z)时为奇函数；当 φ＝kπ(k∈Z)时为偶函数；对称轴方程可由 ωx＋φ＝kπ()求得．(3)y＝Atan(ωx＋φ)，当 φ＝kπ()时为奇函数．3．三角函数的两种常见变换k Z2,222kk  22kk  ,22kk  2,222kk  22kk  π,0k,02k ,02k22k Z2k Z2k Zk Z(1)y＝sin xy＝sin(ωx＋φ)y＝Asin(ωx＋φ)(A＞0，ω＞0)．y＝Asin(ωx＋φ)(A＞0，ω＞0)．4．三角函数公式(1)同角关系：sin2α＋cos2α＝1，．(2)诱导公式：对于“，的三角函数值”与“α 角的三角函数值”的关系可按下面口诀记忆：奇变偶不变，符号看象限．(3)两角和与差的正弦、余弦、正切公式：；；．(4)二倍角公式：，．(5)辅助角公式：asin x＋bcos x＝sin(x＋φ)，其中．热点一 三角函数的图象00          向左或向右平移个单位A          纵坐标变为原来的 倍横坐标不变sintancos 2k k Zsinsincoscossincoscoscossinsintantantan1tantan sin 22sincos2222cos2cossin2cos1 12sin tanba 【例 1】(1) (2018·清流一中)已知函数，（1）用“五点法”作出这个函数在一个周期内的图象；...