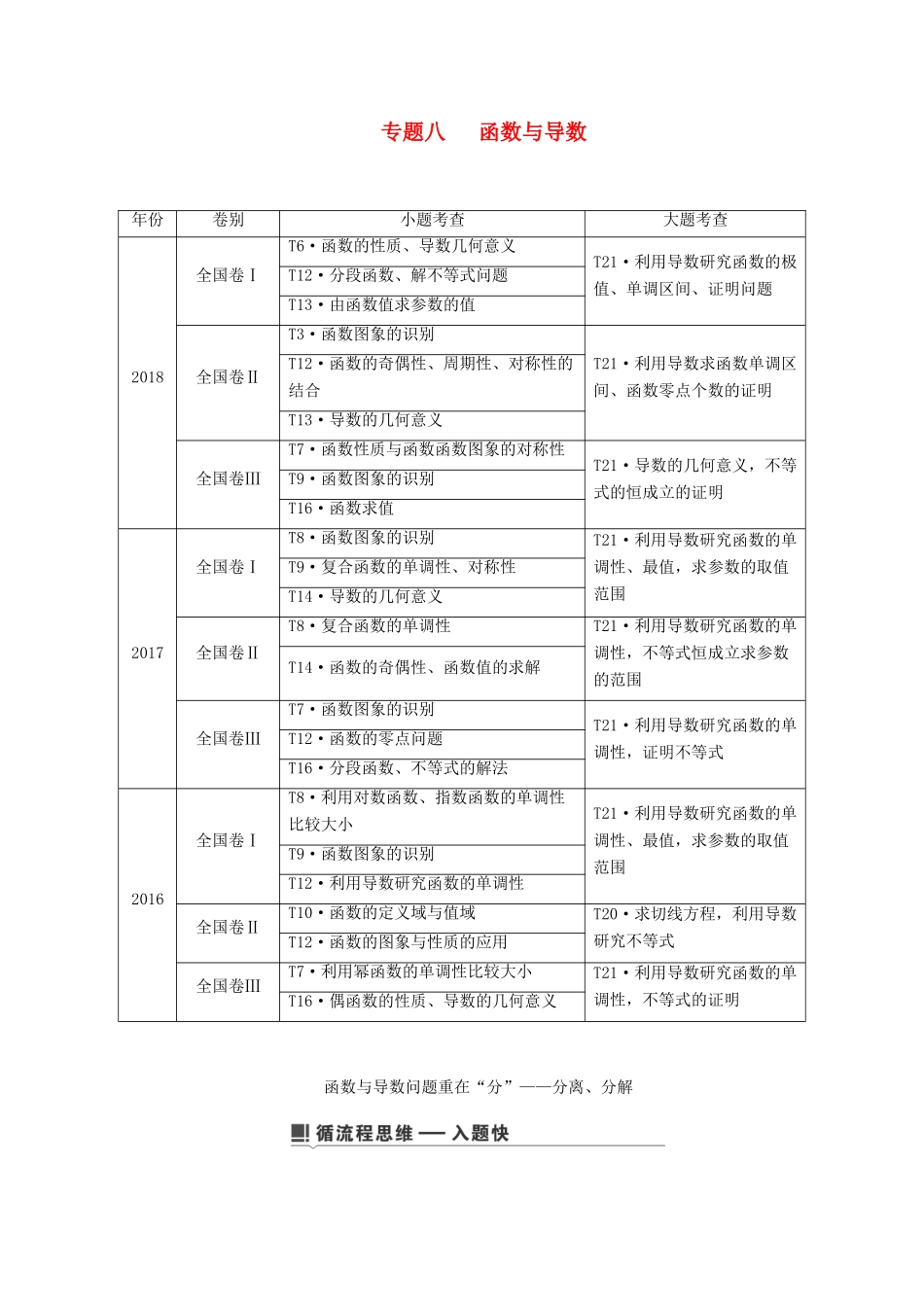
专题八 函数与导数年份卷别小题考查大题考查2018全国卷ⅠT6·函数的性质、导数几何意义T21·利用导数研究函数的极值、单调区间、证明问题T12·分段函数、解不等式问题T13·由函数值求参数的值全国卷ⅡT3·函数图象的识别T21·利用导数求函数单调区间、函数零点个数的证明T12·函数的奇偶性、周期性、对称性的结合T13·导数的几何意义全国卷ⅢT7·函数性质与函数函数图象的对称性T21·导数的几何意义,不等式的恒成立的证明T9·函数图象的识别T16·函数求值2017全国卷ⅠT8·函数图象的识别T21·利用导数研究函数的单调性、最值,求参数的取值范围T9·复合函数的单调性、对称性T14·导数的几何意义全国卷ⅡT8·复合函数的单调性T21·利用导数研究函数的单调性,不等式恒成立求参数的范围T14·函数的奇偶性、函数值的求解全国卷ⅢT7·函数图象的识别T21·利用导数研究函数的单调性,证明不等式T12·函数的零点问题T16·分段函数、不等式的解法2016全国卷ⅠT8·利用对数函数、指数函数的单调性比较大小T21·利用导数研究函数的单调性、最值,求参数的取值范围T9·函数图象的识别T12·利用导数研究函数的单调性全国卷ⅡT10·函数的定义域与值域T20·求切线方程,利用导数研究不等式T12·函数的图象与性质的应用全国卷ⅢT7·利用幂函数的单调性比较大小T21·利用导数研究函数的单调性,不等式的证明T16·偶函数的性质、导数的几何意义函数与导数问题重在“分”——分离、分解 函数与导数问题一般以函数为载体,以导数为工具,重点考查函数的一些性质,如含参函数的单调性、极值或最值的探求与讨论,复杂函数零点的讨论,函数不等式中参数范围的讨论,恒成立和能成立问题的讨论等,是近几年高考试题的命题热点.对于这类综合问题,一般是先求导,再变形、分离或分解出基本函数,再根据题意处理.【典例】 已知函数 f(x)=ln x+x2-(a+1)x.(1)若曲线 y=f(x)在 x=1 处的切线方程为 y=-2,求 f(x)的单调区间;(2)若 x>0 时,<恒成立,求实数 a 的取值范围.[解题示范] (1)函数 f(x)的定义域为(0,+∞).由已知得 f′(x)=+ax-(a+1),则 f′(1)=0.而 f(1)=--1,∴曲线 y=f(x)在 x=1 处的切线方程为 y=--1.∴--1=-2,解得 a=2.∴f(x)=ln x+x2-3x,f′(x)=+2x-3.由 f′(x)>0,得 01,由 f′(x)<0,得