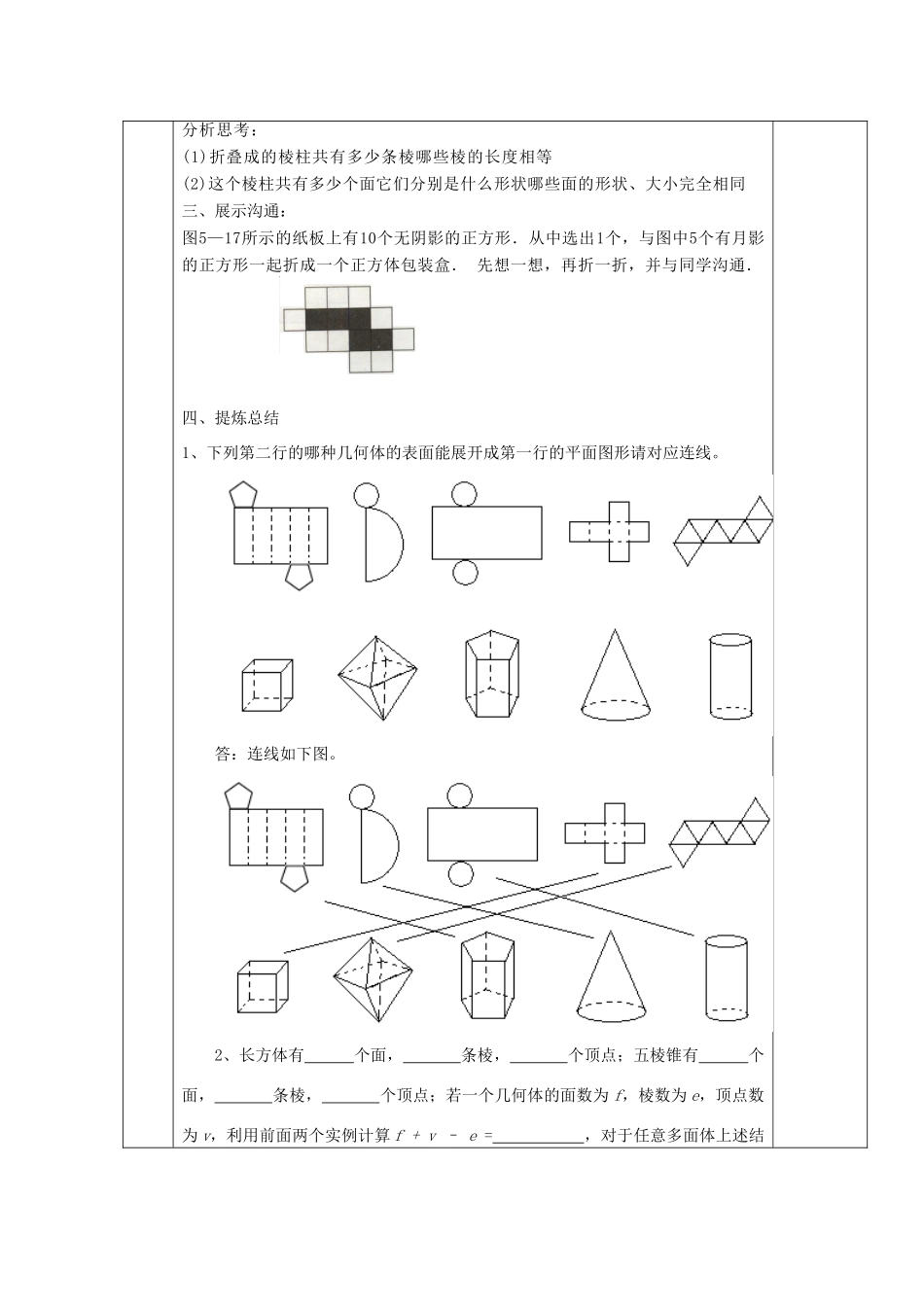
课题 展开与折叠 (2)自主空间学习目标1、进一步认识立体图形与平面图形的关系,了解立体图形可由平面图形围成。2、进一步了解常见几何体的侧面展开图,能根据展开图推断立体模型3、通过折叠的实践操作,在经历和体验图形的转换过程中,初步建立空间观念,进展几何直觉。学习重难点常见几何体的侧面展开图,能根据展开图推断立体模型教学流程预习导航1、 想一想,右图所示的平面图形经过折叠后能否围成一个正方体你能说说理由吗2、 同桌同学合作、沟通:将各自准备的包装纸盒沿某些棱剪开,观察展开图的形状,看看它由哪些平面图形构成再将展开图复原为包装纸盒,从中体会立体图形与平面图形的关系.合作探究一、动手操作把下图中的图形沿虚线折叠,得到3个几何体.(1) 书P132练一练:1(2)数学补充习题P60:1 二、例题分析在下图中,哪些图形沿虚线折叠可以围成(面与面之间不重叠)一个棱柱形的包装盒 先想一想,再动手折一折,验证你的想法.分析思考:(1)折叠成的棱柱共有多少条棱哪些棱的长度相等(2)这个棱柱共有多少个面它们分别是什么形状哪些面的形状、大小完全相同三、展示沟通:图5—17所示的纸板上有10个无阴影的正方形.从中选出1个,与图中5个有月影的正方形一起折成一个正方体包装盒. 先想一想,再折一折,并与同学沟通.四、提炼总结1、下列第二行的哪种几何体的表面能展开成第一行的平面图形请对应连线。答:连线如下图。2、长方体有 个面, 条棱, 个顶点;五棱锥有 个面, 条棱, 个顶点;若一个几何体的面数为 f,棱数为 e,顶点数为 v,利用前面两个实例计算 f + v – e = ,对于任意多面体上述结论都成立吗答:(引出著名的“欧拉公式”)当堂达标1.下列四个平面图形中,不能折叠成无盖的长方体盒子的是( )(A) (B) (C) 2、下列图形是一些多面体的平面展开图,说出这些多面体的名称。 3、下列平面图经过折叠后不能围成正方体的是 ( )4、一个几何体的顶点数是 9,棱数是 16,面数应是 。5、一只蜘蛛在一个正方体的顶点 A 处,一只蚊子在正方体的顶点 B 出,如图所示,现在蜘蛛想尽快地捉到这只蚊子,那么它所走的最短路线是怎样的,在图上画出来,这样的最短路线有几条 学习反思:参考答案5.3 展开与折叠(2) 1、A 2、三棱锥 三棱柱 四棱锥 四棱柱 3、B 4、9 5、6 条图略