高考数学 考点一遍过 专题15 三角函数的图象与性质（含解析）理试题VIP免费

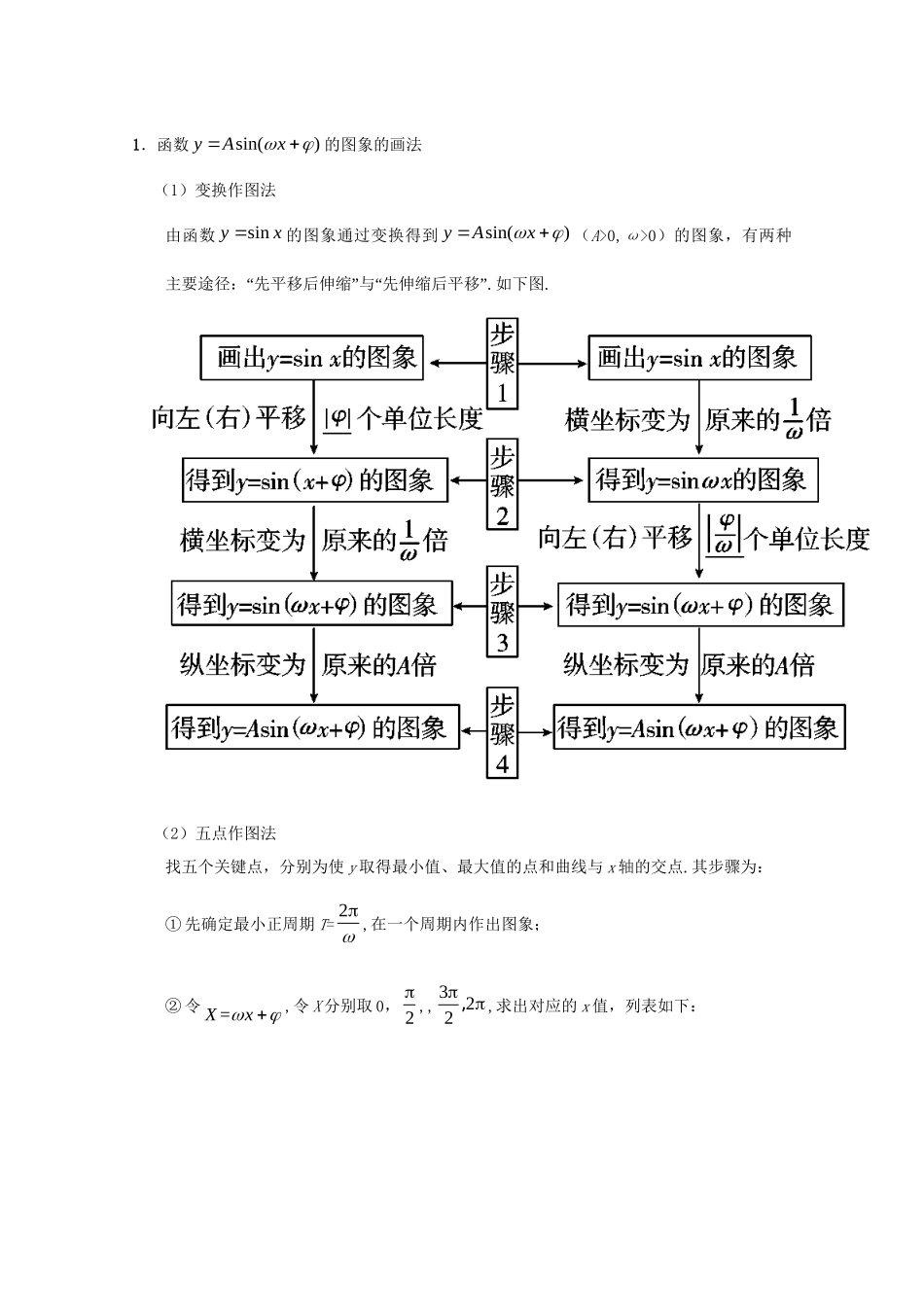
考点15三角函数的图象与性质（1）能画出y=sinx，y=cosx，y=tanx的图象，了解三角函数的周期性.（2）理解正弦函数、余弦函数在[0,2π]上的性质（如单调性、最大值和最小值、以及与x轴的交点等），理解正切函数在,22内的单调性.（3）了解函数sin()yAx的物理意义；能画出sin()yAx的图象，了解参数,,A对函数图象变化的影响.（4）了解三角函数是描述周期变化现象的重要函数模型，会用三角函数解决一些简单实际问题.一、正弦函数sinyx,余弦函数cosyx,正切函数tanyx的图象与性质函数sinyxcosyxtanyx图象定义域RR,2xxkkZ值域1,11,1R最值当π2π2xkkZ时，max1y；当2xkkZ时，max1y；既无最大值，也无最小值当22xkkZ时，min1y．当2xkkZ时，min1y．周期性最小正周期为2最小正周期为2最小正周期为奇偶性sinsinxx,奇函数coscosxx，偶函数tantanxx，奇函数单调性在[2,2]()22kkkZ上是增函数；在3[2,2]()22kkkZ上是减函数．在2,2kkkZ上是增函数；在2,2kkkZ上是减函数．在(,)()22kkkZ上是增函数．对称性对称中心(,0)()kkZ；对称轴2xkkZ，既是中心对称图形又是轴对称图形.对称中心(,0)()2kkZ；对称轴xkkZ，既是中心对称图形又是轴对称图形.对称中心(,0)()2kkZ；无对称轴，是中心对称图形但不是轴对称图形.二、函数sin()yAx的图象与性质1．函数sin()yAx的图象的画法（1）变换作图法由函数sinyx的图象通过变换得到sin()yAx（A>0,ω>0）的图象，有两种“”“”主要途径：先平移后伸缩与先伸缩后平移.如下图.（2）五点作图法找五个关键点，分别为使y取得最小值、最大值的点和曲线与x轴的交点.其步骤为：①先确定最小正周期T=2,在一个周期内作出图象；②令=Xx,令X分别取0，2,,322,,求出对应的x值，列表如下：由此可得五个关键点；③描点画图，再利用函数的周期性把所得简图向左右分别扩展，从而得到sin()yAx的简图.2．函数sin()yAx（A>0,ω>0）的性质（1）奇偶性：=k时，函数sin()yAx为奇函数；=2k时，函数sin()yAx为偶函数.（2）周期性：sin()yAx存在周期性，其最小正周期为T=2.（3）单调性：根据y=sint和t=x的单调性来研究，由+22,22kxkkZ得单调增区间；由+22,22kxkkZ得单调减区间.（4）对称性：利用y=sinx的对称中心为(,0)()kkZ求解，令xkkΖ，求得x.利用y=sinx的对称轴为()2xkkZ求解，令+2xkkΖ，得其对称轴.3．函数sin()yAx（A>0,ω>0）的物理意义当函数sin()yAx（A>0,ω>0,[0,)x）表示一个简谐振动量时，则A叫做振幅，T=2叫做周期，f=12πT叫做频率,x叫做相位，x=0时的相位叫做初相.三、三角函数的综合应用（1）函数sin()yAx，cos()yAx的定义域均为R；函数tan()yAx的定义域均为ππ{|,}2kxxkZ.（2）函数sin()yAx，cos()yAx的最大值为||A，最小值为||A；函数tan()yAx的值域为R.（3）函数sin()yAx，cos()yAx的最小正周期为2π；函数tan()yAx的最小正周期为π．（4）对于sinyAx，当且仅当πkkZ时为奇函数，当且仅当ππ2kkZ时为偶函数；对于cosyAx，当且仅当ππ2kkZ时为奇函数，当且仅当πkkZ时为偶函数；对于tanyAx，当且仅当π2kkZ时为奇函数．（5）函数sin0,0yAxA的单调递增区间由不等式ππ2π2π(22kxkk)Z来确定，单调递减区间由不等式π3π2π2π22kxkkZ来确定；...