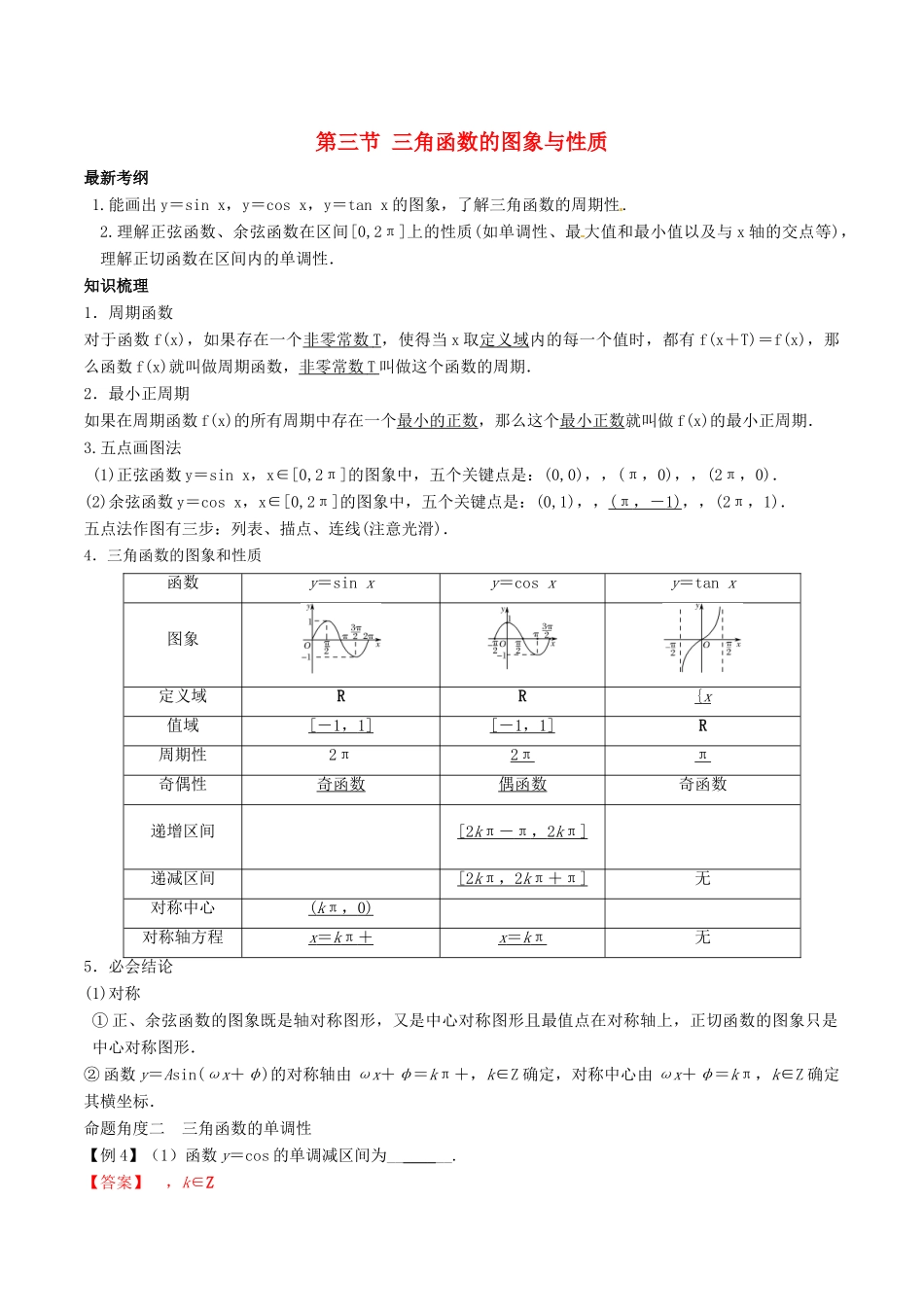
第三节 三角函数的图象与性质最新考纲 1.能画出 y=sin x,y=cos x,y=tan x 的图象,了解三角函数的周期性.2.理解正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最 大值和最小值以及与 x 轴的交点等),理解正切函数在区间内的单调性.知识梳理1.周期函数对于函数 f(x),如果存在一个非零常数 T ,使得当 x 取定义域内的每一个值时,都有 f(x+T)=f(x),那么函数 f(x)就叫做周期函数,非零常数 T 叫做这个函数的周期.2.最小正周期如果在周期函数 f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做 f(x)的最小正周期.3.五点画图法 (1)正弦函数 y=sin x,x∈[0,2π]的图象中,五个关键点是:(0,0),,(π,0),,(2π,0).(2)余弦函数 y=cos x,x∈[0,2π]的图象中,五个关键点是:(0,1),,(π ,- 1) ,,(2π,1).五点法作图有三步:列表、描点、连线(注意光滑).4.三角函数的图象和性质函数y=sin xy=cos xy=tan x图象定义域RR{ x 值域[ - 1 , 1] [ - 1 , 1] R周期性2π2ππ奇偶性奇函数偶函数奇函数递增区间 [2 k π - π , 2 k π] 递减区间[2 k π , 2 k π + π] 无对称中心( k π , 0) 对称轴方程x = k π + x = k π 无5.必会结论(1)对称① 正、余弦函数的图象既是轴对称图形,又是中心对称图形且最值点在对称轴上,正切函数的图象只是中心对称图形.② 函数 y=Asin(ωx+φ)的对称轴由 ωx+φ=kπ+,k∈Z 确定,对称中心由 ωx+φ=kπ,k∈Z 确定其横坐标. 命题角度二 三角函数的单调性【例 4】(1)函数 y=cos 的单调减区间为________.【答案】 ,k∈Z【解析】 y=cos,∴由 2kπ≤2x-≤2kπ+π 得+kπ≤x≤π+kπ,k∈Z,∴函数的单调减区间为,k∈Z.(2)函数 f(x)=sin 的单调递减区间为________.【答案】(k∈Z).(3)若 f(x)=2sin ωx+1(ω>0)在区间上是增函数,则 ω 的取值范围是________.【答案】0<ω≤.【解析】 法一 由 2kπ-≤ωx≤2kπ+,k∈Z,得 f(x)的增区间是(k∈Z).因为 f(x)在上是增函数,所以⊆.所以-≥-且≤,所以 ω∈.法二 因为 x∈,ω>0.所以 ωx∈,又 f(x)在区间上是增函数,所以⊆,则又 ω>0,得 0<ω≤.法三 因为 f(x)在区间上是增函数,故原点到-,的距离不超过,即得 T≥,即≥,又 ω>0,得 0<ω≤.规律方法 (1...